Deep Learning LSTM ANN Machine Learning Data Science Python

Hurricane Path Finder

105 minute read

Data Preparation

Our goal is to use this data to produce a predictive model that will determine future storm parameters with an acceptable level of accuracy. To do so we explore a number of regression and neural network models and evaluate their performance when fitting this dataset.

Data Source

The data used in this project is sourced from National Oceanic and Atmospheric Administration’s HURDAT2 dataset. This dataset contains parameters from observed hurricanes from 1851 to 2023 such as storm category, wind speed, barometric pressure, and center location, collected in six hour periods.

Analysis:

Regression Models

Six regression models, Linear Regression, Stochastic Gradient Descent, Decision Tree Regressor, Random Forest Regressor, Gradient Boosting Regressor, and Support Vector Machine Regression, were applied to the HURDAT dataset in order to predict a hurricane’s track coordinates. These models were applied with and without Principal Component Analysis (PCA) to reduce the feature dimension. The performance of each model was measured by calculating the RMSE and R2 the predicted latitude and longitude values. Of these models the Random Forest model performed best in estimating latitude and longitude with RMSE and R2 values of 0.032 and 0.675 for latitude and 0.03 and 0.725 for longitude when PCA was applied.

Neural Network Models

ANN Models

In our first trial, we used a simple ANN model with 3 hidden layers. The features used for this part are pressure, wind, radii of wind with 64 kt, and the categorical variables.The accuracy of the model is not bad, and the learning curve shows a rapid convergence. In the second model, we added more features corresponding to a sequence of location measurements before feeding this new dataset to the same neural network. RMSE was again measured to evaluate the models. Here we found that the initial model RMSE was 2.3 and 1.4 for the learning and validation data. While this was suitably low it does indicate notable underfitting of the data. Incorporating more historical data in the second model showed significant improvements with RMSE values as low as 0.4 and 0.2 for the testing and training data and much less underfitting.

LSTM Model

Long Short-Term Memory (LSTM) models are a category of neural networks that include feedback connections allowing them to retrain information from sequential datasets.Once the data was prepared a very simple model consisting of one LSTM layer with 50 neurons and a regular densely-connected layer for the output was built. The model was trained over 200 epochs. The resulting learning curve shows that the RMSE reached a minimum of 0.21 without any indication of over or under-fitting. To evaluate the model’s effectiveness it was applied to storm AL152023. Like the training dataset, groups of 4 timesteps were used to predict the storm’s next set of parameters along the complete track. Here we found that the RMSE of the predicted latitude and longitude values were 0.015 and 0.022 respectively. The modeled track follows the observed track fairly closely and retains its characteristics.

References [1] NOAA. The Atlantic hurricane database. https://www.nhc.noaa.gov/data/#hurdat (Accessed on Aug 11, 2024)

import cartopy
import pandas as pd
import numpy as np

import matplotlib.pyplot as plt
import seaborn as sns
import pyproj
import geopy.distance
import cartopy.crs as ccrs

from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras.callbacks import LearningRateScheduler
import tensorflow.keras.backend as K

import warnings
warnings.filterwarnings("ignore")

url='https://www.nhc.noaa.gov/data/hurdat/hurdat2-1851-2023-051124.txt'

Refer to the docs for explanation on the variables: https://www.nhc.noaa.gov/data/hurdat/hurdat2-format-atl-1851-2021.pdf

import requests
raw_data = requests.get(url)
raw_data.status_code

200

url_content = raw_data.content
with open('dataset.txt','wb') as local_file:
  local_file.write(url_content)

#this dictionary temporarily holds the data about each hurricane
clean_data = {}

with open('dataset.txt') as local_file:

  dataset = local_file.readlines()
  curr_id = None
  i = 0

  for row in dataset: # should be a while to iterate over an arbitrary number of events

    columns = row.split()
    clean_line = [i.strip(',') for i in columns]

    if len(clean_line)==3: #treat line as an identifier
      curr_id = clean_line[0]
      clean_data[curr_id] = {'name':clean_line[1],'events':[]}
      rows = int(clean_line[2])
      i = 0
    elif i<rows: #treat line as an event
      clean_data[curr_id]['events'].append(clean_line)
      i+=1
    if i==rows: #finished reading all events for an identifier
      i=0

df = pd.DataFrame.from_dict(clean_data,orient='index').reset_index()
df = df.rename(columns={'index':'id','events':'event'})
df.head()
id name event
0 AL011851 UNNAMED [[18510625, 0000, , HU, 28.0N, 94.8W, 80, -999...
1 AL021851 UNNAMED [[18510705, 1200, , HU, 22.2N, 97.6W, 80, -999...
2 AL031851 UNNAMED [[18510710, 1200, , TS, 12.0N, 60.0W, 50, -999...
3 AL041851 UNNAMED [[18510816, 0000, , TS, 13.4N, 48.0W, 40, -999...
4 AL051851 UNNAMED [[18510913, 0000, , TS, 32.5N, 73.5W, 50, -999... 
df = df.explode('event',ignore_index=True)
df.head()
id name event
0 AL011851 UNNAMED [18510625, 0000, , HU, 28.0N, 94.8W, 80, -999,...
1 AL011851 UNNAMED [18510625, 0600, , HU, 28.0N, 95.4W, 80, -999,...
2 AL011851 UNNAMED [18510625, 1200, , HU, 28.0N, 96.0W, 80, -999,...
3 AL011851 UNNAMED [18510625, 1800, , HU, 28.1N, 96.5W, 80, -999,...
4 AL011851 UNNAMED [18510625, 2100, L, HU, 28.2N, 96.8W, 80, -999... 
event_labels =['X'+str(i) for i in range(21)]
#added column labels starting with a letter, otherwise they will be named only with a number

df_events = pd.DataFrame(df['event'].to_list(),columns=event_labels)

df_events.head()
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 ... X11 X12 X13 X14 X15 X16 X17 X18 X19 X20
0 18510625 0000 HU 28.0N 94.8W 80 -999 -999 -999 ... -999 -999 -999 -999 -999 -999 -999 -999 -999 -999
1 18510625 0600 HU 28.0N 95.4W 80 -999 -999 -999 ... -999 -999 -999 -999 -999 -999 -999 -999 -999 -999
2 18510625 1200 HU 28.0N 96.0W 80 -999 -999 -999 ... -999 -999 -999 -999 -999 -999 -999 -999 -999 -999
3 18510625 1800 HU 28.1N 96.5W 80 -999 -999 -999 ... -999 -999 -999 -999 -999 -999 -999 -999 -999 -999
4 18510625 2100 L HU 28.2N 96.8W 80 -999 -999 -999 ... -999 -999 -999 -999 -999 -999 -999 -999 -999 -999

5 rows × 21 columns

df = pd.concat([df[['id','name']],df_events],axis=1)

df['year']=pd.to_datetime(df['X0']).dt.year
df['month']=pd.to_datetime(df['X0']).dt.month
df['day']=pd.to_datetime(df['X0']).dt.strftime('%d')
df=df.replace('-999',0)

df.head()
id name X0 X1 X2 X3 X4 X5 X6 X7 ... X14 X15 X16 X17 X18 X19 X20 year month day
0 AL011851 UNNAMED 18510625 0000 HU 28.0N 94.8W 80 0 ... 0 0 0 0 0 0 0 1851 6 25
1 AL011851 UNNAMED 18510625 0600 HU 28.0N 95.4W 80 0 ... 0 0 0 0 0 0 0 1851 6 25
2 AL011851 UNNAMED 18510625 1200 HU 28.0N 96.0W 80 0 ... 0 0 0 0 0 0 0 1851 6 25
3 AL011851 UNNAMED 18510625 1800 HU 28.1N 96.5W 80 0 ... 0 0 0 0 0 0 0 1851 6 25
4 AL011851 UNNAMED 18510625 2100 L HU 28.2N 96.8W 80 0 ... 0 0 0 0 0 0 0 1851 6 25

5 rows × 26 columns

#rename column name
df.rename(columns={'X4':'latitude', 'X5':'longitude'}, inplace=True)

def clean_coordinate(original):
  cleaned = float(original[:-1])
  if str(original[-1:]) in ('S','W'):
    cleaned = cleaned * -1
  return cleaned

df['latitude'] = df.apply(lambda x: clean_coordinate(x.latitude), axis=1)
df['longitude'] = df.apply(lambda x: clean_coordinate(x.longitude), axis=1)
df.head()
id name X0 X1 X2 X3 latitude longitude X6 X7 ... X14 X15 X16 X17 X18 X19 X20 year month day
0 AL011851 UNNAMED 18510625 0000 HU 28.0 -94.8 80 0 ... 0 0 0 0 0 0 0 1851 6 25
1 AL011851 UNNAMED 18510625 0600 HU 28.0 -95.4 80 0 ... 0 0 0 0 0 0 0 1851 6 25
2 AL011851 UNNAMED 18510625 1200 HU 28.0 -96.0 80 0 ... 0 0 0 0 0 0 0 1851 6 25
3 AL011851 UNNAMED 18510625 1800 HU 28.1 -96.5 80 0 ... 0 0 0 0 0 0 0 1851 6 25
4 AL011851 UNNAMED 18510625 2100 L HU 28.2 -96.8 80 0 ... 0 0 0 0 0 0 0 1851 6 25

5 rows × 26 columns

Model Building: Neural Network

In this model, we use a NN with three hidden layers. The parameters used for training are the indipendent variables shown above, and the target variables are the “next” longitude and latitude variables.

cols = {'X1':'Time',
        'X2':'RiD',
        'X3':'Status of system',
        'X6':'Maximum sustained wind',
        'X7':'Minimum Pressure',
        'X8':'34 WR NE',
        'X9':'34 WR SE',
        'X10':'34 WR SW',
        'X11':'34 WR NW',
        'X12':'50 WR NE',
        'X13':'50 WR SE',
        'X14':'50 WR SW',
        'X15':'50 WR NW',
        'X16':'64 WR NE',
        'X17':'64 WR SE',
        'X18':'64 WR SW',
        'X19':'64 WR NW',
        'X20':'RMW'}
df_NN = df.rename(columns=cols)

df_NN.head()
id name X0 Time RiD Status of system latitude longitude Maximum sustained wind Minimum Pressure ... 50 WR SW 50 WR NW 64 WR NE 64 WR SE 64 WR SW 64 WR NW RMW year month day
0 AL011851 UNNAMED 18510625 0000 HU 28.0 -94.8 80 0 ... 0 0 0 0 0 0 0 1851 6 25
1 AL011851 UNNAMED 18510625 0600 HU 28.0 -95.4 80 0 ... 0 0 0 0 0 0 0 1851 6 25
2 AL011851 UNNAMED 18510625 1200 HU 28.0 -96.0 80 0 ... 0 0 0 0 0 0 0 1851 6 25
3 AL011851 UNNAMED 18510625 1800 HU 28.1 -96.5 80 0 ... 0 0 0 0 0 0 0 1851 6 25
4 AL011851 UNNAMED 18510625 2100 L HU 28.2 -96.8 80 0 ... 0 0 0 0 0 0 0 1851 6 25

5 rows × 26 columns

Feature Engineering

def One_Step_Forward(DF_2, inc_tan=0): # Making the future coordinate_features.
    DF = DF_2.copy()
    longs = []
    lats = []
    dt = []
    T = []
    wr_tan = []

    for i in range(len(DF)):
        long_n=[];lat_n=[];T_n=[];dt_n=0;tan_n=[];
        if (i<len(DF)-1) and (DF.iloc[i+1]['name'] == DF.iloc[i]['name']):
            if inc_tan==0:
                lat_n =  DF.iloc[i+1]['latitude']
                long_n = DF.iloc[i+1]['longitude']
                T_n = DF.iloc[i+1]['Time']


                t1_n = float(DF.iloc[i+1]['Time'][:2]) + float(DF.iloc[i+1]['Time'][-2:])/60
                t0_n = float(DF.iloc[i]['Time'][:2]) + float(DF.iloc[i]['Time'][-2:])/60
                dt_n = t1_n - t0_n
                if dt_n<0: dt_n = dt_n + 24
            elif inc_tan==1: tan_n = DF.iloc[i+1]['WR_tan']

        else:
            if inc_tan==0:
                lat_n =  DF.iloc[i]['latitude']
                long_n = DF.iloc[i]['longitude']
                T_n = DF.iloc[i]['Time']
                dt_n = 0

            elif inc_tan==1: tan_n=1000

        longs.append(long_n)
        lats.append(lat_n)
        dt.append(dt_n)
        T.append(T_n)
        wr_tan.append(tan_n)

    return (longs,lats,dt,T,wr_tan)


def velocity(DF_2,n=4): #Making velocity features.
    DF = DF_2[['name','Time','latitude','longitude']].copy()
    VXs = []
    VYs = []
    for i in range(n):
        osf = One_Step_Forward(DF,0)
        VX = (np.array(osf[0]) - np.array(DF['longitude']))/(np.array(osf[2]))
        VY = (np.array(osf[1]) - np.array(DF['latitude']))/(np.array(osf[2]))
        VXs.append(list(VX))
        VYs.append(list(VY))

        T = osf[3]
        DF = pd.DataFrame({'Time':T, 'name' : DF['name'], 'latitude': osf[1],'longitude':osf[0]})

    return (VXs,VYs)


def tan(DF_2,n=4): #Making future wind_tangent features.
    DF = DF_2[['name','WR_tan']].copy()
    tans = []
    for i in range(n):
        osf = One_Step_Forward(DF,1)
        tan = np.array(osf[4]) - np.array(DF['WR_tan'])
        tans.append(list(tan))

    return tans

def distance(x): # Measuring how much the hurricane moved
    d = np.sqrt((x['latitude']-x['latitude_1'])**2 + (x['longitude']-x['longitude_1'])**2)

    return d

def theta(x): # The angle of hurricane motion.
    d = np.sqrt((x['latitude']-x['latitude_1'])**2 + (x['longitude']-x['longitude_1'])**2)
    dx = x['longitude_1']-x['longitude']
    dy = x['latitude_1']-x['latitude']

    return np.arctan2(dy,dx)

def speed(x): #Speed
    v =np.absolute(x['Delta']/x['Delta_t'])
    return v

def WR_tan(x): # Tan of "wind direction"

    W_NE_SW = float(x['64 WR NE']) - float(x['64 WR SW'])
    W_NW_SE = float(x['64 WR NW']) - float(x['64 WR SE'])

    return np.arctan2(W_NE_SW,W_NW_SE)

def other(s): # Imputing the categorical variable.
    r=s
    if s=='': r='Others'
    return r

df_direction = df_NN[df_NN['year']>= 1950] # Only the data after 1950, where people sarted to 'name' hurricanes
df_direction.reset_index(drop=True, inplace=True)
df_direction['WR_tan'] = df_direction.apply(WR_tan,axis=1)

one_step = One_Step_Forward(df_direction)
df_direction['latitude_1'] = one_step[1] # The latitude in the next measurement.
df_direction['longitude_1'] = one_step[0] # The latitude in the next measurement.
df_direction['Delta_t'] = one_step[2] # The time difference between the two measurements.
df_direction['Delta'] = df_direction[['latitude','longitude','latitude_1','longitude_1']].apply(distance, axis=1) # The distance the hurricane moved between the twp models.
df_direction['Theta'] = df_direction[['latitude','longitude','latitude_1','longitude_1']].apply(theta, axis=1)
df_direction['Speed'] = df_direction[['Delta','Delta_t']].apply(speed, axis=1) # Speed and angle features.

df_direction['RiD'] = df_direction['RiD'].apply(lambda x: other(x))# Imputing RiD

nums = ['Maximum sustained wind', 'Minimum Pressure',
       '34 WR NE', '34 WR SE', '34 WR SW', '34 WR NW', '50 WR NE', '50 WR SE',
       '50 WR SW', '50 WR NW', '64 WR NE', '64 WR SE', '64 WR SW', '64 WR NW',
       'RMW','latitude','longitude','latitude_1','longitude_1','Speed','Delta_t','Delta','Theta']
cats = ['Status of system','RiD']
target = ['Delta','Theta']

for f in nums:
    df_direction[f] = df_direction[f].apply(float)

df_direction.drop(['id','year','month','day','X0'], axis=1, inplace=True)
df_direction = df_direction[(df_direction['Maximum sustained wind']>0) & (df_direction['Minimum Pressure']>0)] # Natural constrain on the pressure and wind speed.

df_direction = df_direction[['name', 'RiD', 'Status of system', 'latitude', 'longitude',
       'Maximum sustained wind', 'Minimum Pressure', '34 WR NE', '34 WR SE',
       '34 WR SW', '34 WR NW', '50 WR NE', '50 WR SE', '50 WR SW', '50 WR NW',
       '64 WR NE', '64 WR SE', '64 WR SW', '64 WR NW', 'RMW', 'Time', 'WR_tan',
       'latitude_1', 'longitude_1', 'Delta_t', 'Delta', 'Theta', 'Speed']] # Standard column order



print('New dataframe shape: ',df_direction.shape)
df_direction.head()

New dataframe shape:  (23161, 28)
name RiD Status of system latitude longitude Maximum sustained wind Minimum Pressure 34 WR NE 34 WR SE 34 WR SW ... 64 WR NW RMW Time WR_tan latitude_1 longitude_1 Delta_t Delta Theta Speed
7 ABLE Others TS 22.0 -63.2 55.0 997.0 0.0 0.0 0.0 ... 0.0 0.0 1800 0.0 22.7 -63.8 6.0 0.921954 2.279423 0.153659
8 ABLE Others TS 22.7 -63.8 60.0 995.0 0.0 0.0 0.0 ... 0.0 0.0 0000 0.0 23.1 -64.6 6.0 0.894427 2.677945 0.149071
10 ABLE Others TS 23.4 -65.4 60.0 995.0 0.0 0.0 0.0 ... 0.0 0.0 1200 0.0 23.9 -66.0 6.0 0.781025 2.446854 0.130171
11 ABLE Others HU 23.9 -66.0 65.0 989.0 0.0 0.0 0.0 ... 0.0 0.0 1800 0.0 24.4 -66.2 6.0 0.538516 1.951303 0.089753
14 ABLE Others HU 25.2 -66.8 70.0 987.0 0.0 0.0 0.0 ... 0.0 0.0 1200 0.0 25.5 -67.5 6.0 0.761577 2.736701 0.126930

5 rows × 28 columns

Exploratory Data Analysis

fig, axes = plt.subplots(1,2,figsize=(13,5),sharey=True)
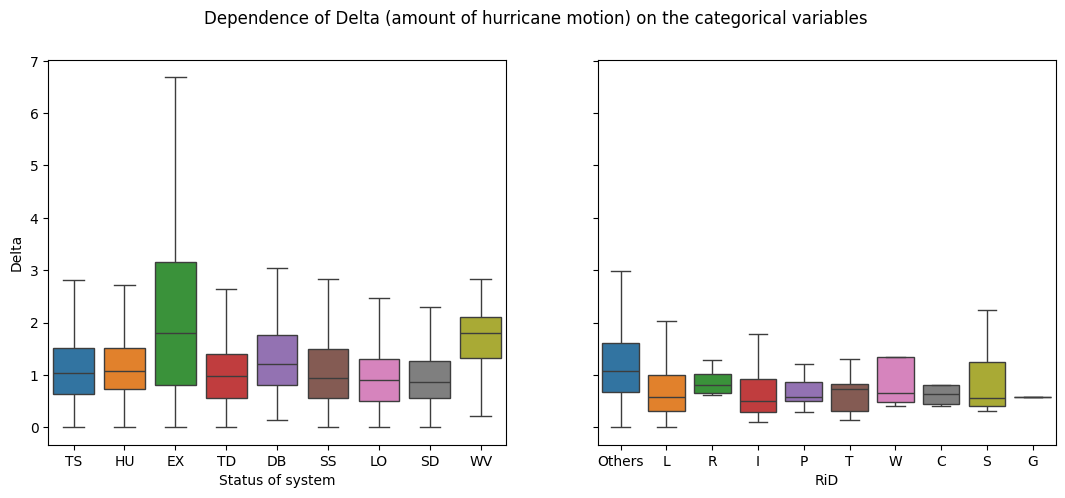
fig.suptitle('Dependence of Delta (amount of hurricane motion) on the categorical variables')

sns.boxplot(ax = axes[0], x='Status of system', y='Delta', data=df_direction, showfliers=False, hue='Status of system')
sns.boxplot(ax = axes[1], x='RiD', y='Delta', data=df_direction, showfliers=False,hue='RiD')

plt.show()

png

fig, axes = plt.subplots(1,2,figsize=(13,5),sharey=True)
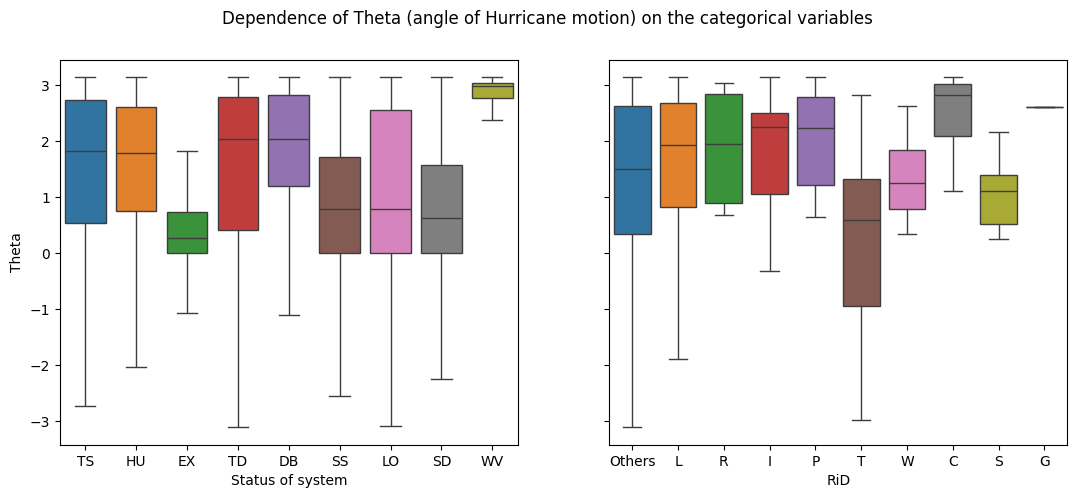
fig.suptitle('Dependence of Theta (angle of Hurricane motion) on the categorical variables')

sns.boxplot(ax = axes[0], x='Status of system', y='Theta', data=df_direction, showfliers=False, hue='Status of system')
sns.boxplot(ax = axes[1], x='RiD', y='Theta', data=df_direction, showfliers=False, hue='RiD')

plt.show()

png

plt.figure(figsize=(30,10))

sns.pairplot(df_direction, x_vars = list(df_direction.columns[3:-8]), y_vars = ['Delta','Theta'])
plt.suptitle('Correlation of Delta and Theta on the numerical variables')

plt.show()

<Figure size 3000x1000 with 0 Axes>

png

df_direction[['latitude', 'longitude',
       'Maximum sustained wind', 'Minimum Pressure','34 WR NE', '34 WR SE',
       '34 WR SW', '34 WR NW', '50 WR NE', '50 WR SE', '50 WR SW', '50 WR NW',
       '64 WR NE', '64 WR SE', '64 WR SW', '64 WR NW', 'RMW','Delta', 'Theta']].corr()[['Delta', 'Theta']].iloc[2:-2]
Delta Theta
Maximum sustained wind 0.007849 0.119953
Minimum Pressure -0.025064 -0.074603
34 WR NE 0.029998 0.017404
34 WR SE 0.064346 -0.036151
34 WR SW 0.064182 -0.087196
34 WR NW 0.021928 -0.016919
50 WR NE 0.025872 0.041630
50 WR SE 0.058866 -0.005343
50 WR SW 0.049487 -0.026482
50 WR NW 0.016102 0.010373
64 WR NE 0.003725 0.067844
64 WR SE 0.030645 0.029762
64 WR SW 0.020989 0.022814
64 WR NW -0.001705 0.059143
RMW -0.005327 -0.029384

Explanation:

The plots show:

1 - Plots trajectory (both delta and theta) depends on the categorical variables.

2 - Delta shows correltion with ‘Maximum sustained wind’ and ‘Minimum Pressure’, ‘latitutde’ and ‘longitude’.

3 - Theta shows correltion with with ‘WR …’ variables.

Model Attempt 1

independent_vars = ['Maximum sustained wind', 'Minimum Pressure','64 WR NE', '64 WR SE', '64 WR SW', '64 WR NW',
                    'latitude','longitude'] + cats
X = df_direction[independent_vars]
y = df_direction[target]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

print('X_train.shape before pipeline: ',X_train.shape)
print('X_test.shape before pipeline: ',X_test.shape)

print('y_train.shape before pipeline: ',y_train.shape)
print('y_test.shape before pipeline: ',y_test.shape)


#pipelines:
cat_ohe = ('ohe',OneHotEncoder(sparse=False, handle_unknown='ignore'))
pipeline_cat = Pipeline([cat_ohe])
transformer_cat = [('cats',pipeline_cat,cats)]

num_scaler = ('sc', StandardScaler())
pipeline_num = Pipeline([num_scaler])
transformer_num = [('num',pipeline_num,independent_vars[:-2])]


ct = ColumnTransformer(transformers = transformer_cat + transformer_num)


X_train = ct.fit_transform(X_train)
X_test = ct.transform(X_test)

print('X_train.shape after pipeline: ',X_train.shape)
print('X_test.shape after pipeline: ',X_test.shape)

print('y_train.shape after pipeline: ',y_train.shape)
print('y_test.shape after pipeline: ',y_test.shape)

X_train.shape before pipeline:  (18528, 10)
X_test.shape before pipeline:  (4633, 10)
y_train.shape before pipeline:  (18528, 2)
y_test.shape before pipeline:  (4633, 2)
X_train.shape after pipeline:  (18528, 27)
X_test.shape after pipeline:  (4633, 27)
y_train.shape after pipeline:  (18528, 2)
y_test.shape after pipeline:  (4633, 2)

def simple_model_1(initializer='he_normal', activation='elu'): # Use relu as base activation function
    return tf.keras.Sequential([layers.Dense(10, activation=None, input_shape=(27,), kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(32, activation=None, kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(32, activation=None, kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(32, activation=None, kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(2, activation='linear', kernel_initializer=tf.keras.initializers.glorot_normal())])


def my_learning_rate(epoch, prev_lrate):
    return prev_lrate*(2**(-0.09))

lrs = LearningRateScheduler(my_learning_rate)

#init = tf.initializers.he_normal()
#activate = 'elu'

# Run model
optimizer = tf.keras.optimizers.SGD(0.9)#.Adam(lr=100, beta_1=0.1, beta_2=0.999)
model = simple_model_1()
model.compile(optimizer=optimizer, loss='Huber', metrics=['RootMeanSquaredError'])
model.fit(X_train, y_train, epochs=300, batch_size=3200, validation_data=(X_test, y_test), callbacks=[lrs])


Epoch 1/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 3s 73ms/step - RootMeanSquaredError: 2.7006 - loss: 1.0415 - val_RootMeanSquaredError: 1.5340 - val_loss: 0.5711 - learning_rate: 0.8456
Epoch 2/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.5490 - loss: 0.5743 - val_RootMeanSquaredError: 1.5444 - val_loss: 0.5637 - learning_rate: 0.7944
Epoch 3/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.5127 - loss: 0.5077 - val_RootMeanSquaredError: 1.4795 - val_loss: 0.5243 - learning_rate: 0.7464
Epoch 4/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.2370 - loss: 0.4872 - val_RootMeanSquaredError: 1.4469 - val_loss: 0.4657 - learning_rate: 0.7012
Epoch 5/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0243 - loss: 0.4533 - val_RootMeanSquaredError: 1.4429 - val_loss: 0.4520 - learning_rate: 0.6588
Epoch 6/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.0554 - loss: 0.4580 - val_RootMeanSquaredError: 1.4432 - val_loss: 0.4456 - learning_rate: 0.6190
Epoch 7/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7863 - loss: 0.4523 - val_RootMeanSquaredError: 1.4413 - val_loss: 0.4518 - learning_rate: 0.5816
Epoch 8/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.0027 - loss: 0.4443 - val_RootMeanSquaredError: 1.4361 - val_loss: 0.4436 - learning_rate: 0.5464
Epoch 9/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.5767 - loss: 0.4588 - val_RootMeanSquaredError: 1.4376 - val_loss: 0.4435 - learning_rate: 0.5133
Epoch 10/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.0301 - loss: 0.4469 - val_RootMeanSquaredError: 1.4374 - val_loss: 0.4459 - learning_rate: 0.4823
Epoch 11/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.9911 - loss: 0.4591 - val_RootMeanSquaredError: 1.4339 - val_loss: 0.4420 - learning_rate: 0.4531
Epoch 12/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.7633 - loss: 0.4400 - val_RootMeanSquaredError: 1.4326 - val_loss: 0.4409 - learning_rate: 0.4257
Epoch 13/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.9237 - loss: 0.4385 - val_RootMeanSquaredError: 1.4287 - val_loss: 0.4381 - learning_rate: 0.4000
Epoch 14/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 2.5516 - loss: 0.4514 - val_RootMeanSquaredError: 1.4289 - val_loss: 0.4355 - learning_rate: 0.3758
Epoch 15/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.1694 - loss: 0.4437 - val_RootMeanSquaredError: 1.4265 - val_loss: 0.4325 - learning_rate: 0.3531
Epoch 16/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.9035 - loss: 0.4381 - val_RootMeanSquaredError: 1.4242 - val_loss: 0.4319 - learning_rate: 0.3317
Epoch 17/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7497 - loss: 0.4387 - val_RootMeanSquaredError: 1.4236 - val_loss: 0.4297 - learning_rate: 0.3116
Epoch 18/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 1.9297 - loss: 0.4415 - val_RootMeanSquaredError: 1.4220 - val_loss: 0.4291 - learning_rate: 0.2928
Epoch 19/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.0254 - loss: 0.4366 - val_RootMeanSquaredError: 1.4210 - val_loss: 0.4281 - learning_rate: 0.2751
Epoch 20/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.6979 - loss: 0.4296 - val_RootMeanSquaredError: 1.4207 - val_loss: 0.4285 - learning_rate: 0.2585
Epoch 21/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.9904 - loss: 0.4590 - val_RootMeanSquaredError: 1.4201 - val_loss: 0.4269 - learning_rate: 0.2428
Epoch 22/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.9233 - loss: 0.4420 - val_RootMeanSquaredError: 1.4191 - val_loss: 0.4275 - learning_rate: 0.2281
Epoch 23/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.8814 - loss: 0.4373 - val_RootMeanSquaredError: 1.4189 - val_loss: 0.4261 - learning_rate: 0.2143
Epoch 24/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.8735 - loss: 0.4469 - val_RootMeanSquaredError: 1.4181 - val_loss: 0.4259 - learning_rate: 0.2014
Epoch 25/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.9815 - loss: 0.4566 - val_RootMeanSquaredError: 1.4162 - val_loss: 0.4249 - learning_rate: 0.1892
Epoch 26/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 1.9744 - loss: 0.4343 - val_RootMeanSquaredError: 1.4176 - val_loss: 0.4248 - learning_rate: 0.1778
Epoch 27/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.3030 - loss: 0.4427 - val_RootMeanSquaredError: 1.4157 - val_loss: 0.4247 - learning_rate: 0.1670
Epoch 28/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step - RootMeanSquaredError: 1.9032 - loss: 0.4401 - val_RootMeanSquaredError: 1.4164 - val_loss: 0.4238 - learning_rate: 0.1569
Epoch 29/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.0573 - loss: 0.4381 - val_RootMeanSquaredError: 1.4155 - val_loss: 0.4236 - learning_rate: 0.1474
Epoch 30/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.7642 - loss: 0.4356 - val_RootMeanSquaredError: 1.4149 - val_loss: 0.4239 - learning_rate: 0.1385
Epoch 31/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.3285 - loss: 0.4453 - val_RootMeanSquaredError: 1.4151 - val_loss: 0.4232 - learning_rate: 0.1301
Epoch 32/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2922 - loss: 0.4402 - val_RootMeanSquaredError: 1.4155 - val_loss: 0.4231 - learning_rate: 0.1223
Epoch 33/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.4850 - loss: 0.4413 - val_RootMeanSquaredError: 1.4151 - val_loss: 0.4231 - learning_rate: 0.1149
Epoch 34/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0449 - loss: 0.4381 - val_RootMeanSquaredError: 1.4142 - val_loss: 0.4229 - learning_rate: 0.1079
Epoch 35/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7545 - loss: 0.4387 - val_RootMeanSquaredError: 1.4146 - val_loss: 0.4228 - learning_rate: 0.1014
Epoch 36/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.8637 - loss: 0.4327 - val_RootMeanSquaredError: 1.4146 - val_loss: 0.4226 - learning_rate: 0.0953
Epoch 37/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8056 - loss: 0.4348 - val_RootMeanSquaredError: 1.4137 - val_loss: 0.4224 - learning_rate: 0.0895
Epoch 38/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.6655 - loss: 0.4332 - val_RootMeanSquaredError: 1.4142 - val_loss: 0.4224 - learning_rate: 0.0841
Epoch 39/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.2224 - loss: 0.4379 - val_RootMeanSquaredError: 1.4142 - val_loss: 0.4223 - learning_rate: 0.0790
Epoch 40/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8707 - loss: 0.4351 - val_RootMeanSquaredError: 1.4140 - val_loss: 0.4222 - learning_rate: 0.0742
Epoch 41/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9800 - loss: 0.4296 - val_RootMeanSquaredError: 1.4140 - val_loss: 0.4221 - learning_rate: 0.0697
Epoch 42/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2435 - loss: 0.4404 - val_RootMeanSquaredError: 1.4135 - val_loss: 0.4220 - learning_rate: 0.0655
Epoch 43/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.5792 - loss: 0.4484 - val_RootMeanSquaredError: 1.4134 - val_loss: 0.4219 - learning_rate: 0.0616
Epoch 44/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.0215 - loss: 0.4307 - val_RootMeanSquaredError: 1.4130 - val_loss: 0.4219 - learning_rate: 0.0578
Epoch 45/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.1210 - loss: 0.4476 - val_RootMeanSquaredError: 1.4129 - val_loss: 0.4218 - learning_rate: 0.0543
Epoch 46/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0532 - loss: 0.4425 - val_RootMeanSquaredError: 1.4132 - val_loss: 0.4217 - learning_rate: 0.0510
Epoch 47/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0064 - loss: 0.4328 - val_RootMeanSquaredError: 1.4130 - val_loss: 0.4217 - learning_rate: 0.0480
Epoch 48/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.5510 - loss: 0.4476 - val_RootMeanSquaredError: 1.4131 - val_loss: 0.4217 - learning_rate: 0.0451
Epoch 49/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.0001 - loss: 0.4382 - val_RootMeanSquaredError: 1.4126 - val_loss: 0.4216 - learning_rate: 0.0423
Epoch 50/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 3.0090 - loss: 0.4574 - val_RootMeanSquaredError: 1.4127 - val_loss: 0.4216 - learning_rate: 0.0398
Epoch 51/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.0080 - loss: 0.4378 - val_RootMeanSquaredError: 1.4126 - val_loss: 0.4215 - learning_rate: 0.0374
Epoch 52/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.2406 - loss: 0.4432 - val_RootMeanSquaredError: 1.4127 - val_loss: 0.4215 - learning_rate: 0.0351
Epoch 53/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.0683 - loss: 0.4345 - val_RootMeanSquaredError: 1.4124 - val_loss: 0.4215 - learning_rate: 0.0330
Epoch 54/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.9715 - loss: 0.4466 - val_RootMeanSquaredError: 1.4123 - val_loss: 0.4214 - learning_rate: 0.0310
Epoch 55/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.9254 - loss: 0.4334 - val_RootMeanSquaredError: 1.4122 - val_loss: 0.4214 - learning_rate: 0.0291
Epoch 56/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.5186 - loss: 0.4427 - val_RootMeanSquaredError: 1.4123 - val_loss: 0.4214 - learning_rate: 0.0274
Epoch 57/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.1943 - loss: 0.4380 - val_RootMeanSquaredError: 1.4122 - val_loss: 0.4213 - learning_rate: 0.0257
Epoch 58/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 2.5156 - loss: 0.4422 - val_RootMeanSquaredError: 1.4122 - val_loss: 0.4213 - learning_rate: 0.0241
Epoch 59/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step - RootMeanSquaredError: 3.0020 - loss: 0.4559 - val_RootMeanSquaredError: 1.4122 - val_loss: 0.4213 - learning_rate: 0.0227
Epoch 60/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step - RootMeanSquaredError: 2.4964 - loss: 0.4447 - val_RootMeanSquaredError: 1.4122 - val_loss: 0.4213 - learning_rate: 0.0213
Epoch 61/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 2.0265 - loss: 0.4319 - val_RootMeanSquaredError: 1.4121 - val_loss: 0.4213 - learning_rate: 0.0200
Epoch 62/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - RootMeanSquaredError: 1.7512 - loss: 0.4327 - val_RootMeanSquaredError: 1.4120 - val_loss: 0.4213 - learning_rate: 0.0188
Epoch 63/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step - RootMeanSquaredError: 2.2249 - loss: 0.4378 - val_RootMeanSquaredError: 1.4119 - val_loss: 0.4212 - learning_rate: 0.0177
Epoch 64/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 2.9764 - loss: 0.4508 - val_RootMeanSquaredError: 1.4119 - val_loss: 0.4212 - learning_rate: 0.0166
Epoch 65/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step - RootMeanSquaredError: 2.5132 - loss: 0.4439 - val_RootMeanSquaredError: 1.4119 - val_loss: 0.4212 - learning_rate: 0.0156
Epoch 66/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 2.1013 - loss: 0.4425 - val_RootMeanSquaredError: 1.4119 - val_loss: 0.4212 - learning_rate: 0.0147
Epoch 67/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step - RootMeanSquaredError: 2.0907 - loss: 0.4402 - val_RootMeanSquaredError: 1.4118 - val_loss: 0.4212 - learning_rate: 0.0138
Epoch 68/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 2.9963 - loss: 0.4570 - val_RootMeanSquaredError: 1.4118 - val_loss: 0.4212 - learning_rate: 0.0129
Epoch 69/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step - RootMeanSquaredError: 2.0858 - loss: 0.4460 - val_RootMeanSquaredError: 1.4118 - val_loss: 0.4212 - learning_rate: 0.0122
Epoch 70/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0427 - loss: 0.4411 - val_RootMeanSquaredError: 1.4118 - val_loss: 0.4212 - learning_rate: 0.0114
Epoch 71/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.1826 - loss: 0.4371 - val_RootMeanSquaredError: 1.4117 - val_loss: 0.4212 - learning_rate: 0.0107
Epoch 72/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.8121 - loss: 0.4371 - val_RootMeanSquaredError: 1.4117 - val_loss: 0.4212 - learning_rate: 0.0101
Epoch 73/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8824 - loss: 0.4300 - val_RootMeanSquaredError: 1.4117 - val_loss: 0.4212 - learning_rate: 0.0095
Epoch 74/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2765 - loss: 0.4399 - val_RootMeanSquaredError: 1.4116 - val_loss: 0.4211 - learning_rate: 0.0089
Epoch 75/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.7815 - loss: 0.4383 - val_RootMeanSquaredError: 1.4116 - val_loss: 0.4211 - learning_rate: 0.0084
Epoch 76/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7931 - loss: 0.4273 - val_RootMeanSquaredError: 1.4116 - val_loss: 0.4211 - learning_rate: 0.0079
Epoch 77/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.4844 - loss: 0.4368 - val_RootMeanSquaredError: 1.4116 - val_loss: 0.4211 - learning_rate: 0.0074
Epoch 78/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.2099 - loss: 0.4388 - val_RootMeanSquaredError: 1.4116 - val_loss: 0.4211 - learning_rate: 0.0069
Epoch 79/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.2382 - loss: 0.4406 - val_RootMeanSquaredError: 1.4116 - val_loss: 0.4211 - learning_rate: 0.0065
Epoch 80/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.5479 - loss: 0.4461 - val_RootMeanSquaredError: 1.4115 - val_loss: 0.4211 - learning_rate: 0.0061
Epoch 81/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9386 - loss: 0.4395 - val_RootMeanSquaredError: 1.4115 - val_loss: 0.4211 - learning_rate: 0.0058
Epoch 82/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.2784 - loss: 0.4398 - val_RootMeanSquaredError: 1.4115 - val_loss: 0.4211 - learning_rate: 0.0054
Epoch 83/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - RootMeanSquaredError: 2.2664 - loss: 0.4382 - val_RootMeanSquaredError: 1.4115 - val_loss: 0.4211 - learning_rate: 0.0051
Epoch 84/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9276 - loss: 0.4367 - val_RootMeanSquaredError: 1.4115 - val_loss: 0.4211 - learning_rate: 0.0048
Epoch 85/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.2112 - loss: 0.4397 - val_RootMeanSquaredError: 1.4115 - val_loss: 0.4211 - learning_rate: 0.0045
Epoch 86/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2002 - loss: 0.4369 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0042
Epoch 87/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2942 - loss: 0.4425 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0040
Epoch 88/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.1081 - loss: 0.4429 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0037
Epoch 89/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 1.8306 - loss: 0.4339 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0035
Epoch 90/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.7764 - loss: 0.4387 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0033
Epoch 91/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.9519 - loss: 0.4370 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0031
Epoch 92/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.5735 - loss: 0.4463 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0029
Epoch 93/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.4758 - loss: 0.4407 - val_RootMeanSquaredError: 1.4114 - val_loss: 0.4211 - learning_rate: 0.0027
Epoch 94/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 1.8390 - loss: 0.4332 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0026
Epoch 95/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9519 - loss: 0.4504 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0024
Epoch 96/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0766 - loss: 0.4385 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0023
Epoch 97/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.5153 - loss: 0.4387 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0021
Epoch 98/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 3.0061 - loss: 0.4531 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0020
Epoch 99/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2387 - loss: 0.4416 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0019
Epoch 100/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step - RootMeanSquaredError: 2.0393 - loss: 0.4390 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0018
Epoch 101/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0328 - loss: 0.4395 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0017
Epoch 102/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 3.0311 - loss: 0.4560 - val_RootMeanSquaredError: 1.4113 - val_loss: 0.4211 - learning_rate: 0.0016
Epoch 103/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.4930 - loss: 0.4422 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0015
Epoch 104/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.1260 - loss: 0.4275 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0014
Epoch 105/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.8131 - loss: 0.4319 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0013
Epoch 106/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - RootMeanSquaredError: 2.9653 - loss: 0.4485 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0012
Epoch 107/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9273 - loss: 0.4410 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0011
Epoch 108/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.8666 - loss: 0.4341 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0011
Epoch 109/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.9866 - loss: 0.4478 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 0.0010
Epoch 110/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.2839 - loss: 0.4432 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 9.4199e-04
Epoch 111/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 3.0009 - loss: 0.4512 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.8502e-04
Epoch 112/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9757 - loss: 0.4484 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.3150e-04
Epoch 113/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.3298 - loss: 0.4464 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.8121e-04
Epoch 114/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.4929 - loss: 0.4469 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.3396e-04
Epoch 115/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - RootMeanSquaredError: 2.2506 - loss: 0.4408 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.8958e-04
Epoch 116/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 1.7589 - loss: 0.4306 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.4787e-04
Epoch 117/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0967 - loss: 0.4398 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.0869e-04
Epoch 118/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.7362 - loss: 0.4316 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.7188e-04
Epoch 119/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 1.7081 - loss: 0.4333 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.3729e-04
Epoch 120/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.7866 - loss: 0.4425 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.0480e-04
Epoch 121/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.4609 - loss: 0.4389 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.7427e-04
Epoch 122/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 2.0085 - loss: 0.4356 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.4559e-04
Epoch 123/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step - RootMeanSquaredError: 1.7507 - loss: 0.4374 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.1864e-04
Epoch 124/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 2.1769 - loss: 0.4329 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.9332e-04
Epoch 125/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step - RootMeanSquaredError: 2.9723 - loss: 0.4485 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.6953e-04
Epoch 126/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step - RootMeanSquaredError: 2.0306 - loss: 0.4377 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.4719e-04
Epoch 127/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 1.8861 - loss: 0.4360 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.2619e-04
Epoch 128/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 1.9971 - loss: 0.4373 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.0646e-04
Epoch 129/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 2.0976 - loss: 0.4361 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.8793e-04
Epoch 130/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 1.7817 - loss: 0.4358 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.7052e-04
Epoch 131/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step - RootMeanSquaredError: 1.7126 - loss: 0.4362 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.5416e-04
Epoch 132/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step - RootMeanSquaredError: 1.7257 - loss: 0.4367 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.3878e-04
Epoch 133/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 3.0192 - loss: 0.4580 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.2434e-04
Epoch 134/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.1211 - loss: 0.4456 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.1078e-04
Epoch 135/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.4784 - loss: 0.4395 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.9803e-04
Epoch 136/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.0858 - loss: 0.4425 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.8605e-04
Epoch 137/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.1770 - loss: 0.4376 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.7480e-04
Epoch 138/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0407 - loss: 0.4420 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.6423e-04
Epoch 139/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.6466 - loss: 0.4305 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.5430e-04
Epoch 140/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7764 - loss: 0.4367 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.4497e-04
Epoch 141/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.8803 - loss: 0.4324 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.3620e-04
Epoch 142/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8031 - loss: 0.4269 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.2796e-04
Epoch 143/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.9691 - loss: 0.4526 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.2022e-04
Epoch 144/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9932 - loss: 0.4543 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.1295e-04
Epoch 145/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 1.6725 - loss: 0.4327 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.0612e-04
Epoch 146/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.8790 - loss: 0.4343 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 9.9703e-05
Epoch 147/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0691 - loss: 0.4409 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 9.3673e-05
Epoch 148/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.1796 - loss: 0.4385 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 8.8008e-05
Epoch 149/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.7004 - loss: 0.4325 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 8.2686e-05
Epoch 150/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.2669 - loss: 0.4434 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 7.7685e-05
Epoch 151/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.3198 - loss: 0.4445 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 7.2987e-05
Epoch 152/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.2809 - loss: 0.4438 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 6.8573e-05
Epoch 153/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - RootMeanSquaredError: 1.8510 - loss: 0.4346 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 6.4426e-05
Epoch 154/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0113 - loss: 0.4381 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 6.0529e-05
Epoch 155/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.0568 - loss: 0.4388 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 5.6869e-05
Epoch 156/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.2456 - loss: 0.4390 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 5.3430e-05
Epoch 157/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.8224 - loss: 0.4380 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 5.0198e-05
Epoch 158/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.5345 - loss: 0.4451 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.7162e-05
Epoch 159/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 2.9591 - loss: 0.4474 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.4310e-05
Epoch 160/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.9688 - loss: 0.4467 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.1630e-05
Epoch 161/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.0559 - loss: 0.4362 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.9113e-05
Epoch 162/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.5432 - loss: 0.4407 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.6747e-05
Epoch 163/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.7894 - loss: 0.4320 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.4525e-05
Epoch 164/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 1.9174 - loss: 0.4328 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.2437e-05
Epoch 165/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.2335 - loss: 0.4429 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.0475e-05
Epoch 166/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.5223 - loss: 0.4439 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.8632e-05
Epoch 167/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7847 - loss: 0.4342 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.6901e-05
Epoch 168/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 2.9684 - loss: 0.4511 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.5274e-05
Epoch 169/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.8794 - loss: 0.4360 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.3745e-05
Epoch 170/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.0021 - loss: 0.4350 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.2309e-05
Epoch 171/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.9371 - loss: 0.4516 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.0960e-05
Epoch 172/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.9532 - loss: 0.4437 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.9692e-05
Epoch 173/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 1.8551 - loss: 0.4349 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.8501e-05
Epoch 174/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 3.0283 - loss: 0.4632 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.7383e-05
Epoch 175/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.5661 - loss: 0.4495 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.6331e-05
Epoch 176/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.0238 - loss: 0.4365 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.5344e-05
Epoch 177/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.5120 - loss: 0.4454 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.4416e-05
Epoch 178/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.0114 - loss: 0.4328 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.3544e-05
Epoch 179/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.0555 - loss: 0.4384 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.2725e-05
Epoch 180/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 1.8761 - loss: 0.4437 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.1955e-05
Epoch 181/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.0459 - loss: 0.4345 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.1232e-05
Epoch 182/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2752 - loss: 0.4414 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.0553e-05
Epoch 183/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9381 - loss: 0.4391 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 9.9147e-06
Epoch 184/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 3.0015 - loss: 0.4491 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 9.3151e-06
Epoch 185/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.9681 - loss: 0.4522 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.7517e-06
Epoch 186/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.9805 - loss: 0.4531 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.2224e-06
Epoch 187/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.6968 - loss: 0.4369 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.7252e-06
Epoch 188/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 3.0086 - loss: 0.4581 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.2580e-06
Epoch 189/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 1.9969 - loss: 0.4441 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 6.8190e-06
Epoch 190/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 2.5186 - loss: 0.4448 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.4066e-06
Epoch 191/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 1.7853 - loss: 0.4377 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 6.0192e-06
Epoch 192/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step - RootMeanSquaredError: 1.8150 - loss: 0.4307 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 5.6551e-06
Epoch 193/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step - RootMeanSquaredError: 2.3124 - loss: 0.4438 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.3131e-06
Epoch 194/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 2.2479 - loss: 0.4402 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.9918e-06
Epoch 195/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 2.0774 - loss: 0.4379 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.6899e-06
Epoch 196/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 2.0509 - loss: 0.4393 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.4063e-06
Epoch 197/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 2.1530 - loss: 0.4349 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 4.1398e-06
Epoch 198/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 2.2900 - loss: 0.4462 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.8894e-06
Epoch 199/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step - RootMeanSquaredError: 2.4843 - loss: 0.4337 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.6542e-06
Epoch 200/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 2.1637 - loss: 0.4301 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.4332e-06
Epoch 201/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.8486 - loss: 0.4353 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.2256e-06
Epoch 202/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.8942 - loss: 0.4372 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.0305e-06
Epoch 203/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.4909 - loss: 0.4369 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.8472e-06
Epoch 204/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.6941 - loss: 0.4295 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.6750e-06
Epoch 205/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.2747 - loss: 0.4399 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.5133e-06
Epoch 206/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.0826 - loss: 0.4411 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.3613e-06
Epoch 207/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9689 - loss: 0.4508 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4210 - learning_rate: 2.2185e-06
Epoch 208/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 3.0213 - loss: 0.4569 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4210 - learning_rate: 2.0843e-06
Epoch 209/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.5206 - loss: 0.4432 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4210 - learning_rate: 1.9583e-06
Epoch 210/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.2105 - loss: 0.4383 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.8398e-06
Epoch 211/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.4868 - loss: 0.4436 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.7286e-06
Epoch 212/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step - RootMeanSquaredError: 2.5555 - loss: 0.4440 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.6240e-06
Epoch 213/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.5234 - loss: 0.4413 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.5258e-06
Epoch 214/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.6189 - loss: 0.4499 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.4335e-06
Epoch 215/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.5625 - loss: 0.4455 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.3468e-06
Epoch 216/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.5557 - loss: 0.4438 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.2654e-06
Epoch 217/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.7109 - loss: 0.4336 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.1888e-06
Epoch 218/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.7084 - loss: 0.4351 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.1170e-06
Epoch 219/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.8148 - loss: 0.4321 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.0494e-06
Epoch 220/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.5046 - loss: 0.4423 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 9.8594e-07
Epoch 221/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.6833 - loss: 0.4273 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 9.2631e-07
Epoch 222/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 2.9770 - loss: 0.4482 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.7029e-07
Epoch 223/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 1.7369 - loss: 0.4286 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.1766e-07
Epoch 224/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.8006 - loss: 0.4284 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.6821e-07
Epoch 225/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.9697 - loss: 0.4323 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.2175e-07
Epoch 226/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8186 - loss: 0.4272 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.7810e-07
Epoch 227/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9943 - loss: 0.4510 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.3709e-07
Epoch 228/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9760 - loss: 0.4507 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.9856e-07
Epoch 229/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.2659 - loss: 0.4420 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.6236e-07
Epoch 230/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9281 - loss: 0.4348 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.2835e-07
Epoch 231/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 1.8656 - loss: 0.4360 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.9640e-07
Epoch 232/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - RootMeanSquaredError: 2.2471 - loss: 0.4407 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.6638e-07
Epoch 233/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.9541 - loss: 0.4539 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.3817e-07
Epoch 234/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step - RootMeanSquaredError: 2.1065 - loss: 0.4447 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.1167e-07
Epoch 235/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8564 - loss: 0.4328 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.8677e-07
Epoch 236/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7987 - loss: 0.4324 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.6338e-07
Epoch 237/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.0058 - loss: 0.4351 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.4141e-07
Epoch 238/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.2254 - loss: 0.4371 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.2076e-07
Epoch 239/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0286 - loss: 0.4355 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.0136e-07
Epoch 240/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 1.9851 - loss: 0.4324 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.8314e-07
Epoch 241/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.0479 - loss: 0.4396 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.6601e-07
Epoch 242/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7939 - loss: 0.4413 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.4992e-07
Epoch 243/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 3.0106 - loss: 0.4527 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.3481e-07
Epoch 244/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.9181 - loss: 0.4415 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.2061e-07
Epoch 245/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 1.9691 - loss: 0.4437 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 2.0727e-07
Epoch 246/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.4895 - loss: 0.4439 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.9473e-07
Epoch 247/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.9577 - loss: 0.4524 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.8296e-07
Epoch 248/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.2470 - loss: 0.4425 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.7189e-07
Epoch 249/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.5096 - loss: 0.4447 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.6150e-07
Epoch 250/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step - RootMeanSquaredError: 1.9775 - loss: 0.4398 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.5173e-07
Epoch 251/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 1.9558 - loss: 0.4402 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.4255e-07
Epoch 252/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step - RootMeanSquaredError: 1.7336 - loss: 0.4354 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.3393e-07
Epoch 253/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 2.6072 - loss: 0.4526 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.2583e-07
Epoch 254/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 3.0377 - loss: 0.4581 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.1822e-07
Epoch 255/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 1.6947 - loss: 0.4330 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.1107e-07
Epoch 256/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step - RootMeanSquaredError: 2.2158 - loss: 0.4396 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 1.0435e-07
Epoch 257/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 2.9848 - loss: 0.4546 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 9.8043e-08
Epoch 258/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 2.9862 - loss: 0.4537 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 9.2114e-08
Epoch 259/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step - RootMeanSquaredError: 1.7483 - loss: 0.4394 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.6543e-08
Epoch 260/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 2.2106 - loss: 0.4395 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 8.1309e-08
Epoch 261/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 1.9221 - loss: 0.4287 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.6392e-08
Epoch 262/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - RootMeanSquaredError: 2.5045 - loss: 0.4436 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 7.1772e-08
Epoch 263/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 1s 45ms/step - RootMeanSquaredError: 2.9755 - loss: 0.4539 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.7431e-08
Epoch 264/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 2.5192 - loss: 0.4398 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 6.3353e-08
Epoch 265/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8494 - loss: 0.4341 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.9522e-08
Epoch 266/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.2821 - loss: 0.4365 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.5922e-08
Epoch 267/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.0260 - loss: 0.4345 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 5.2540e-08
Epoch 268/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.5112 - loss: 0.4427 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.9363e-08
Epoch 269/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 3.0050 - loss: 0.4560 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.6377e-08
Epoch 270/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.7305 - loss: 0.4345 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.3573e-08
Epoch 271/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 1.8956 - loss: 0.4358 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 4.0937e-08
Epoch 272/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.2265 - loss: 0.4423 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.8462e-08
Epoch 273/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - RootMeanSquaredError: 1.7445 - loss: 0.4412 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.6136e-08
Epoch 274/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.9568 - loss: 0.4537 - val_RootMeanSquaredError: 1.4112 - val_loss: 0.4211 - learning_rate: 3.3950e-08
Epoch 275/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 2.0564 - loss: 0.4358 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 3.1897e-08
Epoch 276/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.2770 - loss: 0.4405 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.9968e-08
Epoch 277/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7241 - loss: 0.4357 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.8156e-08
Epoch 278/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.3038 - loss: 0.4443 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.6453e-08
Epoch 279/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step - RootMeanSquaredError: 2.5732 - loss: 0.4469 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.4853e-08
Epoch 280/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step - RootMeanSquaredError: 1.8393 - loss: 0.4358 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.3350e-08
Epoch 281/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.6928 - loss: 0.4311 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.1938e-08
Epoch 282/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7349 - loss: 0.4323 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 2.0611e-08
Epoch 283/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.5360 - loss: 0.4443 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.9365e-08
Epoch 284/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.9775 - loss: 0.4556 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.8193e-08
Epoch 285/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.8606 - loss: 0.4303 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.7093e-08
Epoch 286/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.8574 - loss: 0.4390 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.6059e-08
Epoch 287/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.9021 - loss: 0.4338 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.5088e-08
Epoch 288/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.5022 - loss: 0.4378 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.4176e-08
Epoch 289/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.2846 - loss: 0.4411 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.3318e-08
Epoch 290/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 3.0168 - loss: 0.4526 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.2513e-08
Epoch 291/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step - RootMeanSquaredError: 2.9741 - loss: 0.4493 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.1756e-08
Epoch 292/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.7630 - loss: 0.4348 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.1045e-08
Epoch 293/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step - RootMeanSquaredError: 1.8262 - loss: 0.4346 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 1.0377e-08
Epoch 294/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.5134 - loss: 0.4447 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 9.7496e-09
Epoch 295/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - RootMeanSquaredError: 1.9442 - loss: 0.4404 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 9.1600e-09
Epoch 296/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 2.0092 - loss: 0.4367 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 8.6060e-09
Epoch 297/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step - RootMeanSquaredError: 2.3156 - loss: 0.4432 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 8.0856e-09
Epoch 298/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step - RootMeanSquaredError: 1.7227 - loss: 0.4318 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 7.5966e-09
Epoch 299/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step - RootMeanSquaredError: 1.7825 - loss: 0.4295 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 7.1372e-09
Epoch 300/300
6/6 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step - RootMeanSquaredError: 2.0522 - loss: 0.4350 - val_RootMeanSquaredError: 1.4111 - val_loss: 0.4211 - learning_rate: 6.7055e-09





<keras.src.callbacks.history.History at 0x7d861ecc7bb0>

plt.plot(model.history.history['val_RootMeanSquaredError'], label='Validation RMSE')
plt.plot(model.history.history['RootMeanSquaredError'], label = 'Learning RMSE')

plt.legend()
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.title('Learning curves for NN Model 1')

plt.show()

png

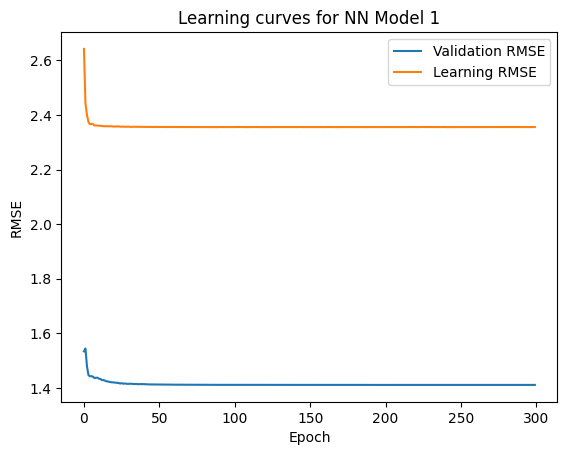
Model Attempt 2 - FIX IT

To improve the performance of the neural network, we add more features corresponding to the sequence of positoins of the /img/posts/Hurricane. Basically, it means if one measures n postions,then we ask whether NN can predict (n+1)th hurricane positons or not.

Since the the time-difference between the measurements are not always 6 hours, the new features are added, are average velocity. So one can multiply these average velocities with the time difference, to find the position in principle.

independent_vars = ['Maximum sustained wind', 'Minimum Pressure','64 WR NE', '64 WR SE', '64 WR SW', '64 WR NW',
                    'latitude','longitude'] + cats

iters = 4

#Tans = tan(df_direction, n=4)
Vs = velocity(df_direction, n=iters)

df_2 = df_direction[independent_vars]
#for i in range(iters):
#    df_2['Tan_'+str(i)] = Tans[i]

for i in range(iters):
    df_2['Vx_'+str(i)] = Vs[0][i]
    df_2['Vy_'+str(i)] = Vs[1][i]

df_2.fillna(0, inplace=True)
df_2.replace([np.inf, -np.inf], 0, inplace=True)
df_2.reset_index(drop=True, inplace=True)

X = df_2[list(df_2.columns[:-2])]
y = df_2[list(df_2.columns[-2:])]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

#Pipeline
cat_ohe = ('ohe',OneHotEncoder(sparse=False, handle_unknown='ignore'))
pipeline_cat = Pipeline([cat_ohe])
transformer_cat = [('cats',pipeline_cat,cats)]

nums = independent_vars[:-2] + list(X.columns[-2*iters+2:])
num_scaler = ('sc', StandardScaler())
pipeline_num = Pipeline([num_scaler])
transformer_num = [('num',pipeline_num,nums)]

ct = ColumnTransformer(transformers = transformer_cat + transformer_num)

X_train = ct.fit_transform(X_train)
X_test = ct.transform(X_test)

print('X_train.shape after pipeline: ',X_train.shape)
print('X_test.shape after pipeline: ',X_test.shape)

print('y_train.shape after pipeline: ',y_train.shape)
print('y_test.shape after pipeline: ',y_test.shape)

X_train.shape after pipeline:  (18528, 33)
X_test.shape after pipeline:  (4633, 33)
y_train.shape after pipeline:  (18528, 2)
y_test.shape after pipeline:  (4633, 2)

def simple_model(initializer='he_uniform', activation='elu'): # Use elu as base activation function
    return tf.keras.Sequential([layers.Dense(33, activation=None, input_shape=(33,), kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(35, activation=None, kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(35, activation=None, kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(35, activation=None, kernel_initializer=initializer),
                                layers.BatchNormalization(trainable=True, scale=True, center=True), # Add BatchNorm
                                layers.Activation(activation), # Add relu activation layer
                                layers.Dense(2, activation='linear', kernel_initializer=tf.keras.initializers.glorot_normal())])

# Run model
optimizer = tf.keras.optimizers.Adam(learning_rate=0.9, beta_1=0.9, beta_2=0.999)
model = simple_model()
model.compile(optimizer=optimizer, loss='Huber', metrics=['RootMeanSquaredError'])
model.fit(X_train, y_train, epochs=300, batch_size=5000, validation_data=(X_test, y_test))#, callbacks=[lrs])

Epoch 1/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 15s 465ms/step - RootMeanSquaredError: 7.4488 - loss: 4.7547 - val_RootMeanSquaredError: 17921.8398 - val_loss: 10411.1680
Epoch 2/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 76ms/step - RootMeanSquaredError: 6.8940 - loss: 5.2487 - val_RootMeanSquaredError: 5395.0459 - val_loss: 2721.0715
Epoch 3/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 72ms/step - RootMeanSquaredError: 4.5877 - loss: 2.8776 - val_RootMeanSquaredError: 4516.1108 - val_loss: 1805.3878
Epoch 4/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - RootMeanSquaredError: 4.3526 - loss: 1.9487 - val_RootMeanSquaredError: 970.2699 - val_loss: 365.5090
Epoch 5/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 72ms/step - RootMeanSquaredError: 3.4563 - loss: 2.2994 - val_RootMeanSquaredError: 810.1371 - val_loss: 355.7299
Epoch 6/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 66ms/step - RootMeanSquaredError: 2.9687 - loss: 1.0866 - val_RootMeanSquaredError: 450.4852 - val_loss: 170.1024
Epoch 7/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - RootMeanSquaredError: 2.3217 - loss: 1.0043 - val_RootMeanSquaredError: 261.0874 - val_loss: 93.9474
Epoch 8/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 74ms/step - RootMeanSquaredError: 1.6845 - loss: 0.9031 - val_RootMeanSquaredError: 35.3243 - val_loss: 13.4167
Epoch 9/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 88ms/step - RootMeanSquaredError: 1.3437 - loss: 0.6310 - val_RootMeanSquaredError: 55.1763 - val_loss: 16.1097
Epoch 10/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 97ms/step - RootMeanSquaredError: 1.1502 - loss: 0.4929 - val_RootMeanSquaredError: 10.9933 - val_loss: 2.9870
Epoch 11/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 116ms/step - RootMeanSquaredError: 0.9229 - loss: 0.3636 - val_RootMeanSquaredError: 9.9476 - val_loss: 3.0795
Epoch 12/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - RootMeanSquaredError: 0.8990 - loss: 0.3560 - val_RootMeanSquaredError: 3.9938 - val_loss: 1.5347
Epoch 13/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 61ms/step - RootMeanSquaredError: 0.7400 - loss: 0.2185 - val_RootMeanSquaredError: 2.4889 - val_loss: 1.0862
Epoch 14/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - RootMeanSquaredError: 0.5729 - loss: 0.1427 - val_RootMeanSquaredError: 2.1575 - val_loss: 0.8417
Epoch 15/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 105ms/step - RootMeanSquaredError: 0.5119 - loss: 0.0974 - val_RootMeanSquaredError: 1.5212 - val_loss: 0.3899
Epoch 16/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 95ms/step - RootMeanSquaredError: 0.4159 - loss: 0.0554 - val_RootMeanSquaredError: 1.1103 - val_loss: 0.2249
Epoch 17/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 102ms/step - RootMeanSquaredError: 0.3463 - loss: 0.0312 - val_RootMeanSquaredError: 0.8685 - val_loss: 0.1997
Epoch 18/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - RootMeanSquaredError: 0.3892 - loss: 0.0282 - val_RootMeanSquaredError: 0.6699 - val_loss: 0.1387
Epoch 19/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 108ms/step - RootMeanSquaredError: 0.3466 - loss: 0.0272 - val_RootMeanSquaredError: 0.5506 - val_loss: 0.1159
Epoch 20/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 98ms/step - RootMeanSquaredError: 0.3700 - loss: 0.0219 - val_RootMeanSquaredError: 0.5412 - val_loss: 0.1309
Epoch 21/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 123ms/step - RootMeanSquaredError: 0.4417 - loss: 0.0179 - val_RootMeanSquaredError: 0.5420 - val_loss: 0.1380
Epoch 22/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 86ms/step - RootMeanSquaredError: 0.2702 - loss: 0.0158 - val_RootMeanSquaredError: 0.5937 - val_loss: 0.1690
Epoch 23/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 74ms/step - RootMeanSquaredError: 0.3648 - loss: 0.0173 - val_RootMeanSquaredError: 0.5816 - val_loss: 0.1634
Epoch 24/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 73ms/step - RootMeanSquaredError: 0.3010 - loss: 0.0154 - val_RootMeanSquaredError: 0.6378 - val_loss: 0.1969
Epoch 25/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 88ms/step - RootMeanSquaredError: 0.4374 - loss: 0.0154 - val_RootMeanSquaredError: 0.5658 - val_loss: 0.1561
Epoch 26/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.4336 - loss: 0.0152 - val_RootMeanSquaredError: 0.6097 - val_loss: 0.1820
Epoch 27/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2896 - loss: 0.0129 - val_RootMeanSquaredError: 0.6064 - val_loss: 0.1806
Epoch 28/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2542 - loss: 0.0127 - val_RootMeanSquaredError: 0.6465 - val_loss: 0.2051
Epoch 29/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.3493 - loss: 0.0151 - val_RootMeanSquaredError: 0.7517 - val_loss: 0.2723
Epoch 30/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step - RootMeanSquaredError: 0.3161 - loss: 0.0197 - val_RootMeanSquaredError: 0.6056 - val_loss: 0.1811
Epoch 31/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step - RootMeanSquaredError: 0.3414 - loss: 0.0132 - val_RootMeanSquaredError: 0.5969 - val_loss: 0.1764
Epoch 32/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.4327 - loss: 0.0137 - val_RootMeanSquaredError: 0.5543 - val_loss: 0.1523
Epoch 33/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.4457 - loss: 0.0186 - val_RootMeanSquaredError: 0.4979 - val_loss: 0.1228
Epoch 34/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step - RootMeanSquaredError: 0.3607 - loss: 0.0183 - val_RootMeanSquaredError: 0.5581 - val_loss: 0.1544
Epoch 35/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step - RootMeanSquaredError: 0.3449 - loss: 0.0130 - val_RootMeanSquaredError: 0.6245 - val_loss: 0.1933
Epoch 36/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.2447 - loss: 0.0124 - val_RootMeanSquaredError: 0.5847 - val_loss: 0.1696
Epoch 37/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2527 - loss: 0.0112 - val_RootMeanSquaredError: 0.5277 - val_loss: 0.1380
Epoch 38/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step - RootMeanSquaredError: 0.3426 - loss: 0.0123 - val_RootMeanSquaredError: 0.5334 - val_loss: 0.1411
Epoch 39/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step - RootMeanSquaredError: 0.2337 - loss: 0.0102 - val_RootMeanSquaredError: 0.4907 - val_loss: 0.1193
Epoch 40/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 71ms/step - RootMeanSquaredError: 0.3457 - loss: 0.0143 - val_RootMeanSquaredError: 0.3726 - val_loss: 0.0683
Epoch 41/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - RootMeanSquaredError: 0.3130 - loss: 0.0195 - val_RootMeanSquaredError: 0.4464 - val_loss: 0.0985
Epoch 42/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 49ms/step - RootMeanSquaredError: 0.2450 - loss: 0.0110 - val_RootMeanSquaredError: 0.5340 - val_loss: 0.1415
Epoch 43/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step - RootMeanSquaredError: 0.3000 - loss: 0.0150 - val_RootMeanSquaredError: 0.4789 - val_loss: 0.1136
Epoch 44/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 92ms/step - RootMeanSquaredError: 0.2796 - loss: 0.0111 - val_RootMeanSquaredError: 0.3920 - val_loss: 0.0758
Epoch 45/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - RootMeanSquaredError: 0.2479 - loss: 0.0104 - val_RootMeanSquaredError: 0.3905 - val_loss: 0.0751
Epoch 46/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 65ms/step - RootMeanSquaredError: 0.2427 - loss: 0.0103 - val_RootMeanSquaredError: 0.4216 - val_loss: 0.0877
Epoch 47/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 67ms/step - RootMeanSquaredError: 0.4363 - loss: 0.0150 - val_RootMeanSquaredError: 0.4733 - val_loss: 0.1109
Epoch 48/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 62ms/step - RootMeanSquaredError: 0.4516 - loss: 0.0210 - val_RootMeanSquaredError: 0.4647 - val_loss: 0.1068
Epoch 49/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 85ms/step - RootMeanSquaredError: 0.3678 - loss: 0.0214 - val_RootMeanSquaredError: 0.3514 - val_loss: 0.0606
Epoch 50/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 57ms/step - RootMeanSquaredError: 0.2431 - loss: 0.0110 - val_RootMeanSquaredError: 0.2360 - val_loss: 0.0266
Epoch 51/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - RootMeanSquaredError: 0.3529 - loss: 0.0164 - val_RootMeanSquaredError: 0.2595 - val_loss: 0.0324
Epoch 52/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 62ms/step - RootMeanSquaredError: 0.2406 - loss: 0.0104 - val_RootMeanSquaredError: 0.3107 - val_loss: 0.0471
Epoch 53/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 74ms/step - RootMeanSquaredError: 0.3397 - loss: 0.0120 - val_RootMeanSquaredError: 0.2864 - val_loss: 0.0400
Epoch 54/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 88ms/step - RootMeanSquaredError: 0.4288 - loss: 0.0121 - val_RootMeanSquaredError: 0.2280 - val_loss: 0.0248
Epoch 55/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 102ms/step - RootMeanSquaredError: 0.4307 - loss: 0.0124 - val_RootMeanSquaredError: 0.2167 - val_loss: 0.0223
Epoch 56/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 89ms/step - RootMeanSquaredError: 0.2442 - loss: 0.0108 - val_RootMeanSquaredError: 0.2433 - val_loss: 0.0285
Epoch 57/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 85ms/step - RootMeanSquaredError: 0.2877 - loss: 0.0103 - val_RootMeanSquaredError: 0.2631 - val_loss: 0.0335
Epoch 58/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 85ms/step - RootMeanSquaredError: 0.4320 - loss: 0.0128 - val_RootMeanSquaredError: 0.2443 - val_loss: 0.0288
Epoch 59/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 127ms/step - RootMeanSquaredError: 0.2805 - loss: 0.0102 - val_RootMeanSquaredError: 0.2328 - val_loss: 0.0260
Epoch 60/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 172ms/step - RootMeanSquaredError: 0.3357 - loss: 0.0108 - val_RootMeanSquaredError: 0.2250 - val_loss: 0.0242
Epoch 61/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 155ms/step - RootMeanSquaredError: 0.2394 - loss: 0.0099 - val_RootMeanSquaredError: 0.2753 - val_loss: 0.0368
Epoch 62/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 105ms/step - RootMeanSquaredError: 0.4567 - loss: 0.0213 - val_RootMeanSquaredError: 0.4243 - val_loss: 0.0891
Epoch 63/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 108ms/step - RootMeanSquaredError: 0.3927 - loss: 0.0566 - val_RootMeanSquaredError: 0.4524 - val_loss: 0.1008
Epoch 64/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 98ms/step - RootMeanSquaredError: 0.4234 - loss: 0.0412 - val_RootMeanSquaredError: 0.1828 - val_loss: 0.0150
Epoch 65/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step - RootMeanSquaredError: 0.3987 - loss: 0.0296 - val_RootMeanSquaredError: 0.2669 - val_loss: 0.0346
Epoch 66/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step - RootMeanSquaredError: 0.2705 - loss: 0.0168 - val_RootMeanSquaredError: 0.1574 - val_loss: 0.0110
Epoch 67/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step - RootMeanSquaredError: 0.3569 - loss: 0.0149 - val_RootMeanSquaredError: 0.2298 - val_loss: 0.0253
Epoch 68/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step - RootMeanSquaredError: 0.4336 - loss: 0.0141 - val_RootMeanSquaredError: 0.1527 - val_loss: 0.0104
Epoch 69/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step - RootMeanSquaredError: 0.2572 - loss: 0.0129 - val_RootMeanSquaredError: 0.2289 - val_loss: 0.0251
Epoch 70/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - RootMeanSquaredError: 0.2979 - loss: 0.0132 - val_RootMeanSquaredError: 0.1403 - val_loss: 0.0086
Epoch 71/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step - RootMeanSquaredError: 0.4306 - loss: 0.0127 - val_RootMeanSquaredError: 0.1741 - val_loss: 0.0140
Epoch 72/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step - RootMeanSquaredError: 0.4288 - loss: 0.0116 - val_RootMeanSquaredError: 0.1572 - val_loss: 0.0111
Epoch 73/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 85ms/step - RootMeanSquaredError: 0.2334 - loss: 0.0094 - val_RootMeanSquaredError: 0.1745 - val_loss: 0.0139
Epoch 74/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 75ms/step - RootMeanSquaredError: 0.2435 - loss: 0.0104 - val_RootMeanSquaredError: 0.1479 - val_loss: 0.0097
Epoch 75/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 117ms/step - RootMeanSquaredError: 0.4361 - loss: 0.0131 - val_RootMeanSquaredError: 0.1880 - val_loss: 0.0166
Epoch 76/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 134ms/step - RootMeanSquaredError: 0.4330 - loss: 0.0125 - val_RootMeanSquaredError: 0.1393 - val_loss: 0.0084
Epoch 77/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 117ms/step - RootMeanSquaredError: 0.4285 - loss: 0.0124 - val_RootMeanSquaredError: 0.1865 - val_loss: 0.0163
Epoch 78/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 113ms/step - RootMeanSquaredError: 0.2279 - loss: 0.0096 - val_RootMeanSquaredError: 0.1468 - val_loss: 0.0095
Epoch 79/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 98ms/step - RootMeanSquaredError: 0.2905 - loss: 0.0122 - val_RootMeanSquaredError: 0.2055 - val_loss: 0.0200
Epoch 80/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 87ms/step - RootMeanSquaredError: 0.4341 - loss: 0.0138 - val_RootMeanSquaredError: 0.1352 - val_loss: 0.0079
Epoch 81/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 82ms/step - RootMeanSquaredError: 0.3430 - loss: 0.0110 - val_RootMeanSquaredError: 0.1745 - val_loss: 0.0141
Epoch 82/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 64ms/step - RootMeanSquaredError: 0.3302 - loss: 0.0105 - val_RootMeanSquaredError: 0.1439 - val_loss: 0.0091
Epoch 83/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 89ms/step - RootMeanSquaredError: 0.4280 - loss: 0.0121 - val_RootMeanSquaredError: 0.1536 - val_loss: 0.0106
Epoch 84/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 95ms/step - RootMeanSquaredError: 0.3328 - loss: 0.0102 - val_RootMeanSquaredError: 0.1484 - val_loss: 0.0099
Epoch 85/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 121ms/step - RootMeanSquaredError: 0.3405 - loss: 0.0104 - val_RootMeanSquaredError: 0.1407 - val_loss: 0.0087
Epoch 86/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 88ms/step - RootMeanSquaredError: 0.4267 - loss: 0.0109 - val_RootMeanSquaredError: 0.1515 - val_loss: 0.0103
Epoch 87/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 72ms/step - RootMeanSquaredError: 0.3355 - loss: 0.0098 - val_RootMeanSquaredError: 0.1432 - val_loss: 0.0091
Epoch 88/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 65ms/step - RootMeanSquaredError: 0.4293 - loss: 0.0115 - val_RootMeanSquaredError: 0.1669 - val_loss: 0.0128
Epoch 89/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - RootMeanSquaredError: 0.2770 - loss: 0.0098 - val_RootMeanSquaredError: 0.1308 - val_loss: 0.0073
Epoch 90/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 76ms/step - RootMeanSquaredError: 0.4278 - loss: 0.0113 - val_RootMeanSquaredError: 0.1568 - val_loss: 0.0111
Epoch 91/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - RootMeanSquaredError: 0.3291 - loss: 0.0096 - val_RootMeanSquaredError: 0.1362 - val_loss: 0.0080
Epoch 92/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 71ms/step - RootMeanSquaredError: 0.3384 - loss: 0.0104 - val_RootMeanSquaredError: 0.1423 - val_loss: 0.0090
Epoch 93/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 90ms/step - RootMeanSquaredError: 0.4316 - loss: 0.0119 - val_RootMeanSquaredError: 0.1460 - val_loss: 0.0094
Epoch 94/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 97ms/step - RootMeanSquaredError: 0.4250 - loss: 0.0110 - val_RootMeanSquaredError: 0.1328 - val_loss: 0.0076
Epoch 95/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 94ms/step - RootMeanSquaredError: 0.2836 - loss: 0.0101 - val_RootMeanSquaredError: 0.1983 - val_loss: 0.0186
Epoch 96/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 81ms/step - RootMeanSquaredError: 0.4441 - loss: 0.0172 - val_RootMeanSquaredError: 0.1550 - val_loss: 0.0108
Epoch 97/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 112ms/step - RootMeanSquaredError: 0.4318 - loss: 0.0124 - val_RootMeanSquaredError: 0.1392 - val_loss: 0.0084
Epoch 98/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 82ms/step - RootMeanSquaredError: 0.2435 - loss: 0.0113 - val_RootMeanSquaredError: 0.1697 - val_loss: 0.0132
Epoch 99/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 93ms/step - RootMeanSquaredError: 0.4334 - loss: 0.0135 - val_RootMeanSquaredError: 0.1527 - val_loss: 0.0104
Epoch 100/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - RootMeanSquaredError: 0.2710 - loss: 0.0093 - val_RootMeanSquaredError: 0.1351 - val_loss: 0.0078
Epoch 101/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.4255 - loss: 0.0113 - val_RootMeanSquaredError: 0.1497 - val_loss: 0.0101
Epoch 102/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 103ms/step - RootMeanSquaredError: 0.4302 - loss: 0.0118 - val_RootMeanSquaredError: 0.1402 - val_loss: 0.0085
Epoch 103/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step - RootMeanSquaredError: 0.2403 - loss: 0.0114 - val_RootMeanSquaredError: 0.1276 - val_loss: 0.0069
Epoch 104/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.3314 - loss: 0.0103 - val_RootMeanSquaredError: 0.1690 - val_loss: 0.0131
Epoch 105/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step - RootMeanSquaredError: 0.4342 - loss: 0.0132 - val_RootMeanSquaredError: 0.1322 - val_loss: 0.0075
Epoch 106/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.4318 - loss: 0.0127 - val_RootMeanSquaredError: 0.1664 - val_loss: 0.0127
Epoch 107/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 67ms/step - RootMeanSquaredError: 0.4342 - loss: 0.0133 - val_RootMeanSquaredError: 0.1466 - val_loss: 0.0095
Epoch 108/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 96ms/step - RootMeanSquaredError: 0.2831 - loss: 0.0102 - val_RootMeanSquaredError: 0.1542 - val_loss: 0.0108
Epoch 109/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 80ms/step - RootMeanSquaredError: 0.4315 - loss: 0.0124 - val_RootMeanSquaredError: 0.1547 - val_loss: 0.0107
Epoch 110/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 65ms/step - RootMeanSquaredError: 0.2261 - loss: 0.0087 - val_RootMeanSquaredError: 0.1306 - val_loss: 0.0073
Epoch 111/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 98ms/step - RootMeanSquaredError: 0.4283 - loss: 0.0110 - val_RootMeanSquaredError: 0.1367 - val_loss: 0.0081
Epoch 112/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 83ms/step - RootMeanSquaredError: 0.4304 - loss: 0.0122 - val_RootMeanSquaredError: 0.1414 - val_loss: 0.0087
Epoch 113/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 66ms/step - RootMeanSquaredError: 0.4371 - loss: 0.0142 - val_RootMeanSquaredError: 0.1597 - val_loss: 0.0117
Epoch 114/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 69ms/step - RootMeanSquaredError: 0.3008 - loss: 0.0131 - val_RootMeanSquaredError: 0.1802 - val_loss: 0.0151
Epoch 115/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 90ms/step - RootMeanSquaredError: 0.2789 - loss: 0.0106 - val_RootMeanSquaredError: 0.1598 - val_loss: 0.0114
Epoch 116/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 77ms/step - RootMeanSquaredError: 0.3172 - loss: 0.0210 - val_RootMeanSquaredError: 0.1602 - val_loss: 0.0115
Epoch 117/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.3464 - loss: 0.0129 - val_RootMeanSquaredError: 0.1646 - val_loss: 0.0123
Epoch 118/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step - RootMeanSquaredError: 0.3394 - loss: 0.0106 - val_RootMeanSquaredError: 0.1263 - val_loss: 0.0068
Epoch 119/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 96ms/step - RootMeanSquaredError: 0.4301 - loss: 0.0121 - val_RootMeanSquaredError: 0.1340 - val_loss: 0.0078
Epoch 120/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 71ms/step - RootMeanSquaredError: 0.2746 - loss: 0.0093 - val_RootMeanSquaredError: 0.1595 - val_loss: 0.0115
Epoch 121/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 80ms/step - RootMeanSquaredError: 0.4236 - loss: 0.0108 - val_RootMeanSquaredError: 0.1413 - val_loss: 0.0088
Epoch 122/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 80ms/step - RootMeanSquaredError: 0.2975 - loss: 0.0134 - val_RootMeanSquaredError: 0.1685 - val_loss: 0.0130
Epoch 123/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step - RootMeanSquaredError: 0.2307 - loss: 0.0100 - val_RootMeanSquaredError: 0.1391 - val_loss: 0.0084
Epoch 124/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 91ms/step - RootMeanSquaredError: 0.3419 - loss: 0.0126 - val_RootMeanSquaredError: 0.1692 - val_loss: 0.0131
Epoch 125/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 81ms/step - RootMeanSquaredError: 0.3360 - loss: 0.0108 - val_RootMeanSquaredError: 0.1264 - val_loss: 0.0068
Epoch 126/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 106ms/step - RootMeanSquaredError: 0.2894 - loss: 0.0108 - val_RootMeanSquaredError: 0.1546 - val_loss: 0.0107
Epoch 127/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 97ms/step - RootMeanSquaredError: 0.3415 - loss: 0.0108 - val_RootMeanSquaredError: 0.1271 - val_loss: 0.0068
Epoch 128/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 119ms/step - RootMeanSquaredError: 0.2290 - loss: 0.0086 - val_RootMeanSquaredError: 0.1475 - val_loss: 0.0097
Epoch 129/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 116ms/step - RootMeanSquaredError: 0.2803 - loss: 0.0094 - val_RootMeanSquaredError: 0.1398 - val_loss: 0.0086
Epoch 130/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 86ms/step - RootMeanSquaredError: 0.3242 - loss: 0.0087 - val_RootMeanSquaredError: 0.1295 - val_loss: 0.0071
Epoch 131/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 88ms/step - RootMeanSquaredError: 0.2347 - loss: 0.0084 - val_RootMeanSquaredError: 0.1459 - val_loss: 0.0094
Epoch 132/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2293 - loss: 0.0082 - val_RootMeanSquaredError: 0.1327 - val_loss: 0.0076
Epoch 133/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.4241 - loss: 0.0098 - val_RootMeanSquaredError: 0.1377 - val_loss: 0.0082
Epoch 134/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - RootMeanSquaredError: 0.4313 - loss: 0.0124 - val_RootMeanSquaredError: 0.1305 - val_loss: 0.0073
Epoch 135/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.4260 - loss: 0.0102 - val_RootMeanSquaredError: 0.1431 - val_loss: 0.0091
Epoch 136/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2590 - loss: 0.0077 - val_RootMeanSquaredError: 0.1295 - val_loss: 0.0071
Epoch 137/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step - RootMeanSquaredError: 0.4282 - loss: 0.0112 - val_RootMeanSquaredError: 0.1255 - val_loss: 0.0067
Epoch 138/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step - RootMeanSquaredError: 0.3293 - loss: 0.0098 - val_RootMeanSquaredError: 0.2110 - val_loss: 0.0212
Epoch 139/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.3573 - loss: 0.0163 - val_RootMeanSquaredError: 0.1468 - val_loss: 0.0095
Epoch 140/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.2517 - loss: 0.0129 - val_RootMeanSquaredError: 0.1514 - val_loss: 0.0103
Epoch 141/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.2354 - loss: 0.0108 - val_RootMeanSquaredError: 0.1439 - val_loss: 0.0091
Epoch 142/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2830 - loss: 0.0114 - val_RootMeanSquaredError: 0.1385 - val_loss: 0.0084
Epoch 143/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step - RootMeanSquaredError: 0.2927 - loss: 0.0106 - val_RootMeanSquaredError: 0.1519 - val_loss: 0.0103
Epoch 144/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.3314 - loss: 0.0098 - val_RootMeanSquaredError: 0.1438 - val_loss: 0.0092
Epoch 145/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 75ms/step - RootMeanSquaredError: 0.4271 - loss: 0.0109 - val_RootMeanSquaredError: 0.1489 - val_loss: 0.0098
Epoch 146/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 59ms/step - RootMeanSquaredError: 0.3383 - loss: 0.0111 - val_RootMeanSquaredError: 0.1573 - val_loss: 0.0112
Epoch 147/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step - RootMeanSquaredError: 0.3319 - loss: 0.0099 - val_RootMeanSquaredError: 0.1423 - val_loss: 0.0089
Epoch 148/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 94ms/step - RootMeanSquaredError: 0.2361 - loss: 0.0087 - val_RootMeanSquaredError: 0.1254 - val_loss: 0.0067
Epoch 149/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 70ms/step - RootMeanSquaredError: 0.4286 - loss: 0.0111 - val_RootMeanSquaredError: 0.1411 - val_loss: 0.0087
Epoch 150/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 76ms/step - RootMeanSquaredError: 0.2746 - loss: 0.0084 - val_RootMeanSquaredError: 0.1321 - val_loss: 0.0075
Epoch 151/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 63ms/step - RootMeanSquaredError: 0.3348 - loss: 0.0090 - val_RootMeanSquaredError: 0.1354 - val_loss: 0.0080
Epoch 152/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step - RootMeanSquaredError: 0.2676 - loss: 0.0079 - val_RootMeanSquaredError: 0.1311 - val_loss: 0.0074
Epoch 153/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 59ms/step - RootMeanSquaredError: 0.2254 - loss: 0.0077 - val_RootMeanSquaredError: 0.1321 - val_loss: 0.0075
Epoch 154/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 59ms/step - RootMeanSquaredError: 0.4250 - loss: 0.0097 - val_RootMeanSquaredError: 0.1433 - val_loss: 0.0091
Epoch 155/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 89ms/step - RootMeanSquaredError: 0.2191 - loss: 0.0076 - val_RootMeanSquaredError: 0.1388 - val_loss: 0.0085
Epoch 156/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step - RootMeanSquaredError: 0.2718 - loss: 0.0082 - val_RootMeanSquaredError: 0.1394 - val_loss: 0.0085
Epoch 157/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step - RootMeanSquaredError: 0.2345 - loss: 0.0081 - val_RootMeanSquaredError: 0.1521 - val_loss: 0.0104
Epoch 158/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.4263 - loss: 0.0103 - val_RootMeanSquaredError: 0.1357 - val_loss: 0.0080
Epoch 159/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.2647 - loss: 0.0080 - val_RootMeanSquaredError: 0.1423 - val_loss: 0.0090
Epoch 160/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - RootMeanSquaredError: 0.2821 - loss: 0.0088 - val_RootMeanSquaredError: 0.1532 - val_loss: 0.0106
Epoch 161/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 72ms/step - RootMeanSquaredError: 0.2728 - loss: 0.0085 - val_RootMeanSquaredError: 0.1247 - val_loss: 0.0065
Epoch 162/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 98ms/step - RootMeanSquaredError: 0.4272 - loss: 0.0113 - val_RootMeanSquaredError: 0.1421 - val_loss: 0.0090
Epoch 163/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 109ms/step - RootMeanSquaredError: 0.3418 - loss: 0.0099 - val_RootMeanSquaredError: 0.1609 - val_loss: 0.0118
Epoch 164/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 107ms/step - RootMeanSquaredError: 0.4327 - loss: 0.0115 - val_RootMeanSquaredError: 0.1266 - val_loss: 0.0068
Epoch 165/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 80ms/step - RootMeanSquaredError: 0.3374 - loss: 0.0094 - val_RootMeanSquaredError: 0.1280 - val_loss: 0.0070
Epoch 166/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 112ms/step - RootMeanSquaredError: 0.2707 - loss: 0.0090 - val_RootMeanSquaredError: 0.1360 - val_loss: 0.0080
Epoch 167/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 82ms/step - RootMeanSquaredError: 0.2371 - loss: 0.0086 - val_RootMeanSquaredError: 0.1509 - val_loss: 0.0102
Epoch 168/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 99ms/step - RootMeanSquaredError: 0.2319 - loss: 0.0083 - val_RootMeanSquaredError: 0.1259 - val_loss: 0.0067
Epoch 169/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 83ms/step - RootMeanSquaredError: 0.2861 - loss: 0.0086 - val_RootMeanSquaredError: 0.1244 - val_loss: 0.0065
Epoch 170/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 114ms/step - RootMeanSquaredError: 0.2417 - loss: 0.0086 - val_RootMeanSquaredError: 0.1584 - val_loss: 0.0114
Epoch 171/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 72ms/step - RootMeanSquaredError: 0.2865 - loss: 0.0100 - val_RootMeanSquaredError: 0.1548 - val_loss: 0.0108
Epoch 172/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.3310 - loss: 0.0089 - val_RootMeanSquaredError: 0.1273 - val_loss: 0.0068
Epoch 173/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.2300 - loss: 0.0090 - val_RootMeanSquaredError: 0.1227 - val_loss: 0.0063
Epoch 174/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.4249 - loss: 0.0098 - val_RootMeanSquaredError: 0.1648 - val_loss: 0.0124
Epoch 175/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.2860 - loss: 0.0099 - val_RootMeanSquaredError: 0.1320 - val_loss: 0.0075
Epoch 176/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2182 - loss: 0.0077 - val_RootMeanSquaredError: 0.1291 - val_loss: 0.0071
Epoch 177/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step - RootMeanSquaredError: 0.2724 - loss: 0.0085 - val_RootMeanSquaredError: 0.1364 - val_loss: 0.0081
Epoch 178/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.4244 - loss: 0.0099 - val_RootMeanSquaredError: 0.1284 - val_loss: 0.0071
Epoch 179/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.3244 - loss: 0.0083 - val_RootMeanSquaredError: 0.1600 - val_loss: 0.0117
Epoch 180/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.3298 - loss: 0.0096 - val_RootMeanSquaredError: 0.1699 - val_loss: 0.0133
Epoch 181/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step - RootMeanSquaredError: 0.2838 - loss: 0.0093 - val_RootMeanSquaredError: 0.1260 - val_loss: 0.0067
Epoch 182/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.4295 - loss: 0.0114 - val_RootMeanSquaredError: 0.1303 - val_loss: 0.0073
Epoch 183/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.2725 - loss: 0.0081 - val_RootMeanSquaredError: 0.1515 - val_loss: 0.0103
Epoch 184/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 76ms/step - RootMeanSquaredError: 0.4262 - loss: 0.0109 - val_RootMeanSquaredError: 0.1387 - val_loss: 0.0085
Epoch 185/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 63ms/step - RootMeanSquaredError: 0.2760 - loss: 0.0084 - val_RootMeanSquaredError: 0.1269 - val_loss: 0.0068
Epoch 186/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 71ms/step - RootMeanSquaredError: 0.2389 - loss: 0.0082 - val_RootMeanSquaredError: 0.1331 - val_loss: 0.0077
Epoch 187/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 49ms/step - RootMeanSquaredError: 0.3243 - loss: 0.0082 - val_RootMeanSquaredError: 0.1415 - val_loss: 0.0088
Epoch 188/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 82ms/step - RootMeanSquaredError: 0.2220 - loss: 0.0076 - val_RootMeanSquaredError: 0.1538 - val_loss: 0.0107
Epoch 189/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step - RootMeanSquaredError: 0.4297 - loss: 0.0111 - val_RootMeanSquaredError: 0.1501 - val_loss: 0.0101
Epoch 190/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step - RootMeanSquaredError: 0.2669 - loss: 0.0084 - val_RootMeanSquaredError: 0.1228 - val_loss: 0.0063
Epoch 191/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 64ms/step - RootMeanSquaredError: 0.2328 - loss: 0.0083 - val_RootMeanSquaredError: 0.1278 - val_loss: 0.0070
Epoch 192/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 65ms/step - RootMeanSquaredError: 0.2767 - loss: 0.0083 - val_RootMeanSquaredError: 0.1335 - val_loss: 0.0077
Epoch 193/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step - RootMeanSquaredError: 0.3321 - loss: 0.0090 - val_RootMeanSquaredError: 0.1541 - val_loss: 0.0108
Epoch 194/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step - RootMeanSquaredError: 0.2464 - loss: 0.0094 - val_RootMeanSquaredError: 0.1448 - val_loss: 0.0093
Epoch 195/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 73ms/step - RootMeanSquaredError: 0.4301 - loss: 0.0109 - val_RootMeanSquaredError: 0.1256 - val_loss: 0.0066
Epoch 196/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step - RootMeanSquaredError: 0.3418 - loss: 0.0110 - val_RootMeanSquaredError: 0.1308 - val_loss: 0.0073
Epoch 197/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.3450 - loss: 0.0108 - val_RootMeanSquaredError: 0.1386 - val_loss: 0.0084
Epoch 198/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.3345 - loss: 0.0093 - val_RootMeanSquaredError: 0.1265 - val_loss: 0.0068
Epoch 199/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step - RootMeanSquaredError: 0.2783 - loss: 0.0084 - val_RootMeanSquaredError: 0.1336 - val_loss: 0.0078
Epoch 200/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.3375 - loss: 0.0088 - val_RootMeanSquaredError: 0.1233 - val_loss: 0.0064
Epoch 201/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.4299 - loss: 0.0102 - val_RootMeanSquaredError: 0.1299 - val_loss: 0.0073
Epoch 202/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.4262 - loss: 0.0098 - val_RootMeanSquaredError: 0.1630 - val_loss: 0.0122
Epoch 203/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - RootMeanSquaredError: 0.4310 - loss: 0.0112 - val_RootMeanSquaredError: 0.1337 - val_loss: 0.0077
Epoch 204/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step - RootMeanSquaredError: 0.2820 - loss: 0.0106 - val_RootMeanSquaredError: 0.1303 - val_loss: 0.0073
Epoch 205/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - RootMeanSquaredError: 0.4293 - loss: 0.0110 - val_RootMeanSquaredError: 0.1419 - val_loss: 0.0089
Epoch 206/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 97ms/step - RootMeanSquaredError: 0.4299 - loss: 0.0104 - val_RootMeanSquaredError: 0.1309 - val_loss: 0.0073
Epoch 207/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 86ms/step - RootMeanSquaredError: 0.3342 - loss: 0.0095 - val_RootMeanSquaredError: 0.1221 - val_loss: 0.0063
Epoch 208/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step - RootMeanSquaredError: 0.3289 - loss: 0.0090 - val_RootMeanSquaredError: 0.1398 - val_loss: 0.0085
Epoch 209/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step - RootMeanSquaredError: 0.3334 - loss: 0.0090 - val_RootMeanSquaredError: 0.1379 - val_loss: 0.0084
Epoch 210/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 71ms/step - RootMeanSquaredError: 0.4268 - loss: 0.0096 - val_RootMeanSquaredError: 0.1245 - val_loss: 0.0065
Epoch 211/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - RootMeanSquaredError: 0.4251 - loss: 0.0097 - val_RootMeanSquaredError: 0.1343 - val_loss: 0.0078
Epoch 212/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 88ms/step - RootMeanSquaredError: 0.3320 - loss: 0.0084 - val_RootMeanSquaredError: 0.1506 - val_loss: 0.0102
Epoch 213/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 76ms/step - RootMeanSquaredError: 0.2198 - loss: 0.0080 - val_RootMeanSquaredError: 0.1256 - val_loss: 0.0066
Epoch 214/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - RootMeanSquaredError: 0.2701 - loss: 0.0091 - val_RootMeanSquaredError: 0.1293 - val_loss: 0.0071
Epoch 215/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 60ms/step - RootMeanSquaredError: 0.2936 - loss: 0.0101 - val_RootMeanSquaredError: 0.1622 - val_loss: 0.0120
Epoch 216/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 67ms/step - RootMeanSquaredError: 0.3328 - loss: 0.0099 - val_RootMeanSquaredError: 0.1335 - val_loss: 0.0077
Epoch 217/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 56ms/step - RootMeanSquaredError: 0.4293 - loss: 0.0113 - val_RootMeanSquaredError: 0.1700 - val_loss: 0.0133
Epoch 218/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 58ms/step - RootMeanSquaredError: 0.2448 - loss: 0.0098 - val_RootMeanSquaredError: 0.1330 - val_loss: 0.0075
Epoch 219/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step - RootMeanSquaredError: 0.2806 - loss: 0.0092 - val_RootMeanSquaredError: 0.1437 - val_loss: 0.0092
Epoch 220/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step - RootMeanSquaredError: 0.2622 - loss: 0.0077 - val_RootMeanSquaredError: 0.1262 - val_loss: 0.0067
Epoch 221/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.2289 - loss: 0.0074 - val_RootMeanSquaredError: 0.1300 - val_loss: 0.0073
Epoch 222/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step - RootMeanSquaredError: 0.3342 - loss: 0.0083 - val_RootMeanSquaredError: 0.1336 - val_loss: 0.0077
Epoch 223/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - RootMeanSquaredError: 0.3271 - loss: 0.0086 - val_RootMeanSquaredError: 0.1330 - val_loss: 0.0076
Epoch 224/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step - RootMeanSquaredError: 0.4272 - loss: 0.0099 - val_RootMeanSquaredError: 0.1245 - val_loss: 0.0065
Epoch 225/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - RootMeanSquaredError: 0.2746 - loss: 0.0081 - val_RootMeanSquaredError: 0.1288 - val_loss: 0.0071
Epoch 226/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step - RootMeanSquaredError: 0.2788 - loss: 0.0079 - val_RootMeanSquaredError: 0.1306 - val_loss: 0.0073
Epoch 227/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step - RootMeanSquaredError: 0.4293 - loss: 0.0098 - val_RootMeanSquaredError: 0.1306 - val_loss: 0.0073
Epoch 228/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 59ms/step - RootMeanSquaredError: 0.2803 - loss: 0.0087 - val_RootMeanSquaredError: 0.1282 - val_loss: 0.0070
Epoch 229/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 55ms/step - RootMeanSquaredError: 0.2083 - loss: 0.0065 - val_RootMeanSquaredError: 0.1249 - val_loss: 0.0066
Epoch 230/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - RootMeanSquaredError: 0.4218 - loss: 0.0094 - val_RootMeanSquaredError: 0.1328 - val_loss: 0.0076
Epoch 231/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.4254 - loss: 0.0094 - val_RootMeanSquaredError: 0.1263 - val_loss: 0.0068
Epoch 232/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.2214 - loss: 0.0072 - val_RootMeanSquaredError: 0.1299 - val_loss: 0.0072
Epoch 233/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.2207 - loss: 0.0071 - val_RootMeanSquaredError: 0.1252 - val_loss: 0.0067
Epoch 234/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.3295 - loss: 0.0084 - val_RootMeanSquaredError: 0.1254 - val_loss: 0.0066
Epoch 235/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.3318 - loss: 0.0082 - val_RootMeanSquaredError: 0.1280 - val_loss: 0.0070
Epoch 236/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.2122 - loss: 0.0070 - val_RootMeanSquaredError: 0.1238 - val_loss: 0.0065
Epoch 237/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.4274 - loss: 0.0097 - val_RootMeanSquaredError: 0.1230 - val_loss: 0.0064
Epoch 238/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 66ms/step - RootMeanSquaredError: 0.2161 - loss: 0.0070 - val_RootMeanSquaredError: 0.1320 - val_loss: 0.0075
Epoch 239/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step - RootMeanSquaredError: 0.3346 - loss: 0.0084 - val_RootMeanSquaredError: 0.1223 - val_loss: 0.0063
Epoch 240/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step - RootMeanSquaredError: 0.4232 - loss: 0.0091 - val_RootMeanSquaredError: 0.1271 - val_loss: 0.0068
Epoch 241/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step - RootMeanSquaredError: 0.3331 - loss: 0.0083 - val_RootMeanSquaredError: 0.1273 - val_loss: 0.0070
Epoch 242/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step - RootMeanSquaredError: 0.2212 - loss: 0.0070 - val_RootMeanSquaredError: 0.1295 - val_loss: 0.0071
Epoch 243/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 73ms/step - RootMeanSquaredError: 0.2620 - loss: 0.0077 - val_RootMeanSquaredError: 0.1306 - val_loss: 0.0074
Epoch 244/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - RootMeanSquaredError: 0.4236 - loss: 0.0091 - val_RootMeanSquaredError: 0.1282 - val_loss: 0.0071
Epoch 245/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 55ms/step - RootMeanSquaredError: 0.3444 - loss: 0.0087 - val_RootMeanSquaredError: 0.1249 - val_loss: 0.0066
Epoch 246/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 87ms/step - RootMeanSquaredError: 0.3243 - loss: 0.0081 - val_RootMeanSquaredError: 0.1379 - val_loss: 0.0083
Epoch 247/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.4240 - loss: 0.0095 - val_RootMeanSquaredError: 0.1354 - val_loss: 0.0080
Epoch 248/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 64ms/step - RootMeanSquaredError: 0.3302 - loss: 0.0089 - val_RootMeanSquaredError: 0.1253 - val_loss: 0.0067
Epoch 249/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.4293 - loss: 0.0099 - val_RootMeanSquaredError: 0.1254 - val_loss: 0.0067
Epoch 250/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - RootMeanSquaredError: 0.2194 - loss: 0.0073 - val_RootMeanSquaredError: 0.1426 - val_loss: 0.0090
Epoch 251/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 64ms/step - RootMeanSquaredError: 0.3376 - loss: 0.0087 - val_RootMeanSquaredError: 0.1247 - val_loss: 0.0065
Epoch 252/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 73ms/step - RootMeanSquaredError: 0.2689 - loss: 0.0087 - val_RootMeanSquaredError: 0.1225 - val_loss: 0.0063
Epoch 253/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step - RootMeanSquaredError: 0.2584 - loss: 0.0071 - val_RootMeanSquaredError: 0.1272 - val_loss: 0.0069
Epoch 254/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step - RootMeanSquaredError: 0.2703 - loss: 0.0075 - val_RootMeanSquaredError: 0.1243 - val_loss: 0.0065
Epoch 255/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - RootMeanSquaredError: 0.4294 - loss: 0.0100 - val_RootMeanSquaredError: 0.1221 - val_loss: 0.0062
Epoch 256/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.3244 - loss: 0.0078 - val_RootMeanSquaredError: 0.1248 - val_loss: 0.0066
Epoch 257/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 78ms/step - RootMeanSquaredError: 0.2312 - loss: 0.0070 - val_RootMeanSquaredError: 0.1268 - val_loss: 0.0069
Epoch 258/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 67ms/step - RootMeanSquaredError: 0.3365 - loss: 0.0085 - val_RootMeanSquaredError: 0.1305 - val_loss: 0.0074
Epoch 259/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - RootMeanSquaredError: 0.2303 - loss: 0.0078 - val_RootMeanSquaredError: 0.1257 - val_loss: 0.0067
Epoch 260/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 95ms/step - RootMeanSquaredError: 0.2829 - loss: 0.0085 - val_RootMeanSquaredError: 0.1218 - val_loss: 0.0062
Epoch 261/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - RootMeanSquaredError: 0.4258 - loss: 0.0098 - val_RootMeanSquaredError: 0.1278 - val_loss: 0.0070
Epoch 262/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - RootMeanSquaredError: 0.2714 - loss: 0.0077 - val_RootMeanSquaredError: 0.1282 - val_loss: 0.0071
Epoch 263/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 1s 61ms/step - RootMeanSquaredError: 0.2249 - loss: 0.0073 - val_RootMeanSquaredError: 0.1263 - val_loss: 0.0067
Epoch 264/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step - RootMeanSquaredError: 0.2633 - loss: 0.0079 - val_RootMeanSquaredError: 0.1362 - val_loss: 0.0081
Epoch 265/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 62ms/step - RootMeanSquaredError: 0.3294 - loss: 0.0088 - val_RootMeanSquaredError: 0.1207 - val_loss: 0.0061
Epoch 266/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.4254 - loss: 0.0103 - val_RootMeanSquaredError: 0.1208 - val_loss: 0.0061
Epoch 267/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.4262 - loss: 0.0098 - val_RootMeanSquaredError: 0.1274 - val_loss: 0.0070
Epoch 268/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step - RootMeanSquaredError: 0.2822 - loss: 0.0082 - val_RootMeanSquaredError: 0.1220 - val_loss: 0.0062
Epoch 269/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.2764 - loss: 0.0079 - val_RootMeanSquaredError: 0.1303 - val_loss: 0.0073
Epoch 270/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.2772 - loss: 0.0080 - val_RootMeanSquaredError: 0.1201 - val_loss: 0.0060
Epoch 271/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.2330 - loss: 0.0076 - val_RootMeanSquaredError: 0.1204 - val_loss: 0.0060
Epoch 272/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.2645 - loss: 0.0073 - val_RootMeanSquaredError: 0.1230 - val_loss: 0.0064
Epoch 273/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step - RootMeanSquaredError: 0.3260 - loss: 0.0078 - val_RootMeanSquaredError: 0.1229 - val_loss: 0.0064
Epoch 274/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.4250 - loss: 0.0093 - val_RootMeanSquaredError: 0.1227 - val_loss: 0.0063
Epoch 275/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.4277 - loss: 0.0100 - val_RootMeanSquaredError: 0.1201 - val_loss: 0.0060
Epoch 276/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.3293 - loss: 0.0083 - val_RootMeanSquaredError: 0.1264 - val_loss: 0.0068
Epoch 277/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.4225 - loss: 0.0093 - val_RootMeanSquaredError: 0.1205 - val_loss: 0.0061
Epoch 278/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.3312 - loss: 0.0082 - val_RootMeanSquaredError: 0.1310 - val_loss: 0.0074
Epoch 279/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.3244 - loss: 0.0083 - val_RootMeanSquaredError: 0.1237 - val_loss: 0.0064
Epoch 280/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step - RootMeanSquaredError: 0.2552 - loss: 0.0072 - val_RootMeanSquaredError: 0.1234 - val_loss: 0.0065
Epoch 281/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.2312 - loss: 0.0077 - val_RootMeanSquaredError: 0.1228 - val_loss: 0.0064
Epoch 282/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.2280 - loss: 0.0071 - val_RootMeanSquaredError: 0.1232 - val_loss: 0.0064
Epoch 283/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.2717 - loss: 0.0081 - val_RootMeanSquaredError: 0.1299 - val_loss: 0.0073
Epoch 284/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.3313 - loss: 0.0086 - val_RootMeanSquaredError: 0.1264 - val_loss: 0.0068
Epoch 285/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.4260 - loss: 0.0098 - val_RootMeanSquaredError: 0.1362 - val_loss: 0.0082
Epoch 286/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.4243 - loss: 0.0097 - val_RootMeanSquaredError: 0.1216 - val_loss: 0.0062
Epoch 287/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step - RootMeanSquaredError: 0.3332 - loss: 0.0081 - val_RootMeanSquaredError: 0.1177 - val_loss: 0.0057
Epoch 288/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step - RootMeanSquaredError: 0.2266 - loss: 0.0071 - val_RootMeanSquaredError: 0.1241 - val_loss: 0.0066
Epoch 289/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step - RootMeanSquaredError: 0.2768 - loss: 0.0081 - val_RootMeanSquaredError: 0.1218 - val_loss: 0.0062
Epoch 290/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.3259 - loss: 0.0079 - val_RootMeanSquaredError: 0.1188 - val_loss: 0.0059
Epoch 291/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.2267 - loss: 0.0075 - val_RootMeanSquaredError: 0.1252 - val_loss: 0.0067
Epoch 292/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.2769 - loss: 0.0081 - val_RootMeanSquaredError: 0.1177 - val_loss: 0.0058
Epoch 293/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - RootMeanSquaredError: 0.4231 - loss: 0.0095 - val_RootMeanSquaredError: 0.1239 - val_loss: 0.0064
Epoch 294/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step - RootMeanSquaredError: 0.3388 - loss: 0.0088 - val_RootMeanSquaredError: 0.1379 - val_loss: 0.0084
Epoch 295/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step - RootMeanSquaredError: 0.4290 - loss: 0.0103 - val_RootMeanSquaredError: 0.1221 - val_loss: 0.0062
Epoch 296/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.2762 - loss: 0.0080 - val_RootMeanSquaredError: 0.1311 - val_loss: 0.0074
Epoch 297/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step - RootMeanSquaredError: 0.2165 - loss: 0.0076 - val_RootMeanSquaredError: 0.1235 - val_loss: 0.0064
Epoch 298/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - RootMeanSquaredError: 0.3397 - loss: 0.0096 - val_RootMeanSquaredError: 0.1297 - val_loss: 0.0071
Epoch 299/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step - RootMeanSquaredError: 0.2670 - loss: 0.0081 - val_RootMeanSquaredError: 0.1254 - val_loss: 0.0067
Epoch 300/300
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step - RootMeanSquaredError: 0.2691 - loss: 0.0078 - val_RootMeanSquaredError: 0.1284 - val_loss: 0.0070





<keras.src.callbacks.history.History at 0x78a2f6d79ff0>

For this model, the RMSE value of the validation set decreased significantly, which shows great improvement in model’s performance. However, the underfitting problem is not resolved.

In the next model two modifications we’ll be considered:

1- in addtion to the sequence of position measurements, we’ll add sequence of wind and pressure measurments.

2- We make a simpler neural network with less number of layers. This hopefully solve the underfitting problem.

plt.plot(model.history.history['val_RootMeanSquaredError'][12:], label='Validation RMSE')
plt.plot(model.history.history['RootMeanSquaredError'][12:], label = 'Learning RMSE')

plt.legend()
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.title('Learning Curve for NN model 2')

plt.show()

png

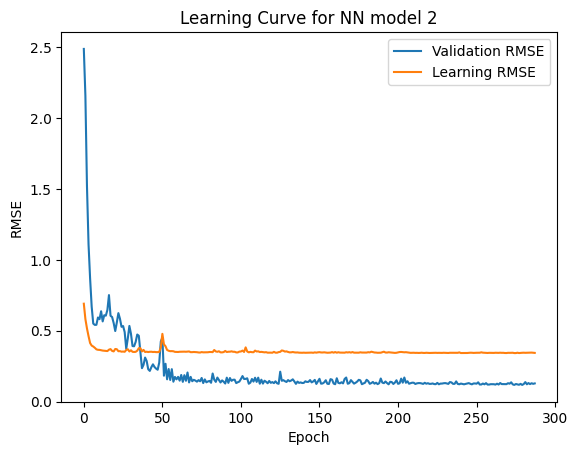
Model Attempt 3

cols = {'X0':'time',
        'X1':'hour',
        'X2':'record identifier',
        'X3':'system status',
        'X6':'maximum sustained wind',
        'X7':'minimum Pressure',
        'X8':'northeastern 34 kt wind radii',
        'X9':'southeastern 34 kt wind radii',
        'X10':'southwestern 34 kt wind radii',
        'X11':'northwestern 34 kt wind radii',
        'X12':'northeastern 50 kt wind radii',
        'X13':'southeastern 50 kt wind radii',
        'X14':'southwestern 50 kt wind radii',
        'X15':'northwestern 50 kt wind radii',
        'X16':'northeastern 64 kt wind radii',
        'X17':'southeastern 64 kt wind radii',
        'X18':'southwestern 64 kt wind radii',
        'X19':'northwestern 64 kt wind radii',
        'X20':'radius of max wind'}

df_NN_3 = df.rename(columns=cols)

df_NN_3['temp'] = df_NN_3.time+' '+df_NN_3.hour
df_NN_3['temp'] = pd.to_datetime(df_NN_3['temp'],format='%Y%m%d %H%M')
df_NN_3.drop(columns=['time','hour'],inplace=True)
df_NN_3.rename(columns={'temp':'time'},inplace=True)
df_NN_3.head()
id name record identifier system status latitude longitude maximum sustained wind minimum Pressure northeastern 34 kt wind radii southeastern 34 kt wind radii ... northwestern 50 kt wind radii northeastern 64 kt wind radii southeastern 64 kt wind radii southwestern 64 kt wind radii northwestern 64 kt wind radii radius of max wind year month day time
0 AL011851 UNNAMED HU 28.0 -94.8 80 0 0 0 ... 0 0 0 0 0 0 1851 6 25 1851-06-25 00:00:00
1 AL011851 UNNAMED HU 28.0 -95.4 80 0 0 0 ... 0 0 0 0 0 0 1851 6 25 1851-06-25 06:00:00
2 AL011851 UNNAMED HU 28.0 -96.0 80 0 0 0 ... 0 0 0 0 0 0 1851 6 25 1851-06-25 12:00:00
3 AL011851 UNNAMED HU 28.1 -96.5 80 0 0 0 ... 0 0 0 0 0 0 1851 6 25 1851-06-25 18:00:00
4 AL011851 UNNAMED L HU 28.2 -96.8 80 0 0 0 ... 0 0 0 0 0 0 1851 6 25 1851-06-25 21:00:00

5 rows × 25 columns

# one hot encoding for the storm status (also was not used)
df_NN_3 = pd.get_dummies(df_NN_3, columns=['system status'], dtype=int)

# remove outlier - likely invalid data
idx = df_NN_3.loc[(df_NN_3.id=="AL081969")&(df_NN_3.longitude==-354.5)].index[0]
df_NN_3.drop(index=idx, inplace=True)

# rename columns to something more mangeable
new_col_names = {
    "latitude":"lat_0",
    "longitude":"lon_0",
    "maximum sustained wind": "max_wind",
    "minimum Pressure": "min_pressure",
    "system status_DB": "DB",
    "system status_EX": "EX",
    "system status_HU": "HU",
    "system status_LO": "LO",
    "system status_SD": "SD",
    "system status_SS": "SS",
    "system status_TD": "TD",
    "system status_TS": "TS",
    "system status_WV": "WV",
}
df_NN_3.rename(columns=new_col_names, inplace=True)

df_NN_3.head()
id name record identifier lat_0 lon_0 max_wind min_pressure northeastern 34 kt wind radii southeastern 34 kt wind radii southwestern 34 kt wind radii ... time DB EX HU LO SD SS TD TS WV
0 AL011851 UNNAMED 28.0 -94.8 80 0 0 0 0 ... 1851-06-25 00:00:00 0 0 1 0 0 0 0 0 0
1 AL011851 UNNAMED 28.0 -95.4 80 0 0 0 0 ... 1851-06-25 06:00:00 0 0 1 0 0 0 0 0 0
2 AL011851 UNNAMED 28.0 -96.0 80 0 0 0 0 ... 1851-06-25 12:00:00 0 0 1 0 0 0 0 0 0
3 AL011851 UNNAMED 28.1 -96.5 80 0 0 0 0 ... 1851-06-25 18:00:00 0 0 1 0 0 0 0 0 0
4 AL011851 UNNAMED L 28.2 -96.8 80 0 0 0 0 ... 1851-06-25 21:00:00 0 0 1 0 0 0 0 0 0

5 rows × 33 columns

Reducing the dimensionality and scaling the data

data_cols = [
    "id",
    "time",
    "lat_0",
    "lon_0",
    "max_wind",
    "min_pressure"
]

df_NN_3 = df_NN_3[data_cols].dropna()

df_NN_3['max_wind'] = df_NN_3['max_wind'].astype('float')
df_NN_3['min_pressure'] = df_NN_3['min_pressure'].astype('float')

# these are the columns that need to be scaled from 0 to 1
scaled_cols = [
    "lat_0",
    "lon_0",
    "max_wind",
    "min_pressure",
]

model_scaled = df_NN_3.copy()
col_mins = {}
col_maxs = {}
for col in scaled_cols:
    col_data = model_scaled[col].values
    col_min = col_data.min()
    col_max = col_data.max()
    scaled_data = (col_data-col_min)/col_max # scale to (0,1)
    model_scaled[col] = scaled_data
    col_mins[col] = col_min
    col_maxs[col] = col_max
model_scaled
id time lat_0 lon_0 max_wind min_pressure
0 AL011851 1851-06-25 00:00:00 0.253012 4.185714 1.084848 0.000000
1 AL011851 1851-06-25 06:00:00 0.253012 4.176190 1.084848 0.000000
2 AL011851 1851-06-25 12:00:00 0.253012 4.166667 1.084848 0.000000
3 AL011851 1851-06-25 18:00:00 0.254217 4.158730 1.084848 0.000000
4 AL011851 1851-06-25 21:00:00 0.255422 4.153968 1.084848 0.000000
... ... ... ... ... ... ...
54744 AL212023 2023-10-23 18:00:00 0.054217 4.369841 0.751515 0.983398
54745 AL212023 2023-10-24 00:00:00 0.062651 4.366667 0.751515 0.983398
54746 AL212023 2023-10-24 01:30:00 0.065060 4.365079 0.751515 0.983398
54747 AL212023 2023-10-24 06:00:00 0.072289 4.360317 0.751515 0.983398
54748 AL212023 2023-10-24 12:00:00 0.078313 4.350794 0.721212 0.983398

54748 rows × 6 columns

"""
The model uses 4 sequential points to predict the 5th. To pass this to the NN each row of the X data needs to contain the four timesteps leading up to the Y data.
"""

storm_ids = model_scaled.id.unique()
window_size = 4
window_cols = ["lat_0","lon_0", "max_wind", "min_pressure"]
windowed_data = pd.DataFrame()

# looping over each storm to ensure data is continuous
for storm_id in storm_ids:
    subset = model_scaled.loc[model_scaled.id == storm_id].copy() # get the data from the current storm
    subset.dropna(inplace=True)
    if len(subset) > window_size: # ensure that the storm has at least 5 timesteps
        # loop over the storm data with a 5 row sliding window
        for idx in range(len(subset) - window_size):
            window = subset.iloc[idx : idx + window_size + 1, :][::-1] # select the window data and reverse the order
            time_diff = window.time.diff().dt.total_seconds().dropna().unique() # get an array of the difference between each time stamp
            # skip this window if there isn't 6 hours between each observation (negative because data is reversed)
            if len(time_diff) > 1 or time_diff[0] != -21600:
                continue
            # shift the data 5 times so that each time step is in the first row of the window dataframe
            for offset in range(1, window_size + 1):
                shifted = window.shift(-offset)
                for col in window_cols:
                    window[f"{col}-{offset}"] = shifted[col] # add the shifted data to the dataframe
            windowed_data = pd.concat([windowed_data, window.iloc[[0]]]) # extract the first row


# separate the windowed data into x and y variables
x_data = windowed_data.copy().drop(columns=window_cols+["id","time"])
y_data = windowed_data[window_cols].copy()

X_train, X_test, y_train, y_test = train_test_split(x_data, y_data, shuffle=True)

# LSTM models xpect the input data to have shape (samples, timesteps, features).
# Since each row is its time step need to add a dimension of length 1 in the middle of the array
X_train = X_train.values.reshape(X_train.shape[0],1,X_train.shape[-1])
X_test = X_test.values.reshape(X_test.shape[0],1,X_test.shape[-1])

# Build the LSTM NN. I was planning to incorporate more layers but the results only worsened.
K.clear_session()
model = keras.Sequential()
model.add(keras.layers.LSTM(50, input_shape=(1,16,))) # 1,16 corresponds to input data shape
model.add(keras.layers.Dense(units=4))
model.compile(loss='Huber', optimizer='adam', metrics=['RootMeanSquaredError'])
model.fit(X_train, y_train, epochs=200, batch_size=1000, validation_data=(X_test, y_test))

Epoch 1/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 3s 19ms/step - RootMeanSquaredError: 2.3325 - loss: 1.1612 - val_RootMeanSquaredError: 1.7535 - val_loss: 0.7689
Epoch 2/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 1.5430 - loss: 0.6579 - val_RootMeanSquaredError: 0.8353 - val_loss: 0.2974
Epoch 3/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.6288 - loss: 0.1847 - val_RootMeanSquaredError: 0.2591 - val_loss: 0.0332
Epoch 4/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - RootMeanSquaredError: 0.2544 - loss: 0.0321 - val_RootMeanSquaredError: 0.2194 - val_loss: 0.0237
Epoch 5/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 13ms/step - RootMeanSquaredError: 0.2083 - loss: 0.0215 - val_RootMeanSquaredError: 0.1834 - val_loss: 0.0164
Epoch 6/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 12ms/step - RootMeanSquaredError: 0.1759 - loss: 0.0153 - val_RootMeanSquaredError: 0.1721 - val_loss: 0.0144
Epoch 7/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - RootMeanSquaredError: 0.1692 - loss: 0.0141 - val_RootMeanSquaredError: 0.1692 - val_loss: 0.0139
Epoch 8/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1687 - loss: 0.0139 - val_RootMeanSquaredError: 0.1670 - val_loss: 0.0135
Epoch 9/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - RootMeanSquaredError: 0.1683 - loss: 0.0136 - val_RootMeanSquaredError: 0.1644 - val_loss: 0.0131
Epoch 10/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - RootMeanSquaredError: 0.1608 - loss: 0.0128 - val_RootMeanSquaredError: 0.1616 - val_loss: 0.0127
Epoch 11/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.1598 - loss: 0.0125 - val_RootMeanSquaredError: 0.1583 - val_loss: 0.0121
Epoch 12/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.1550 - loss: 0.0118 - val_RootMeanSquaredError: 0.1548 - val_loss: 0.0116
Epoch 13/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.1517 - loss: 0.0113 - val_RootMeanSquaredError: 0.1512 - val_loss: 0.0110
Epoch 14/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1462 - loss: 0.0106 - val_RootMeanSquaredError: 0.1471 - val_loss: 0.0104
Epoch 15/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step - RootMeanSquaredError: 0.1453 - loss: 0.0103 - val_RootMeanSquaredError: 0.1435 - val_loss: 0.0099
Epoch 16/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 14ms/step - RootMeanSquaredError: 0.1427 - loss: 0.0099 - val_RootMeanSquaredError: 0.1399 - val_loss: 0.0094
Epoch 17/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 25ms/step - RootMeanSquaredError: 0.1349 - loss: 0.0090 - val_RootMeanSquaredError: 0.1362 - val_loss: 0.0088
Epoch 18/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 18ms/step - RootMeanSquaredError: 0.1316 - loss: 0.0085 - val_RootMeanSquaredError: 0.1323 - val_loss: 0.0083
Epoch 19/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1286 - loss: 0.0081 - val_RootMeanSquaredError: 0.1289 - val_loss: 0.0079
Epoch 20/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 19ms/step - RootMeanSquaredError: 0.1242 - loss: 0.0075 - val_RootMeanSquaredError: 0.1264 - val_loss: 0.0075
Epoch 21/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - RootMeanSquaredError: 0.1243 - loss: 0.0074 - val_RootMeanSquaredError: 0.1241 - val_loss: 0.0073
Epoch 22/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1214 - loss: 0.0070 - val_RootMeanSquaredError: 0.1223 - val_loss: 0.0070
Epoch 23/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1185 - loss: 0.0068 - val_RootMeanSquaredError: 0.1210 - val_loss: 0.0069
Epoch 24/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1158 - loss: 0.0066 - val_RootMeanSquaredError: 0.1198 - val_loss: 0.0067
Epoch 25/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1153 - loss: 0.0066 - val_RootMeanSquaredError: 0.1189 - val_loss: 0.0066
Epoch 26/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1146 - loss: 0.0065 - val_RootMeanSquaredError: 0.1179 - val_loss: 0.0065
Epoch 27/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1128 - loss: 0.0063 - val_RootMeanSquaredError: 0.1170 - val_loss: 0.0064
Epoch 28/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1140 - loss: 0.0062 - val_RootMeanSquaredError: 0.1162 - val_loss: 0.0063
Epoch 29/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1122 - loss: 0.0061 - val_RootMeanSquaredError: 0.1154 - val_loss: 0.0062
Epoch 30/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1082 - loss: 0.0058 - val_RootMeanSquaredError: 0.1148 - val_loss: 0.0061
Epoch 31/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1116 - loss: 0.0060 - val_RootMeanSquaredError: 0.1143 - val_loss: 0.0061
Epoch 32/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1105 - loss: 0.0060 - val_RootMeanSquaredError: 0.1137 - val_loss: 0.0060
Epoch 33/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1074 - loss: 0.0057 - val_RootMeanSquaredError: 0.1134 - val_loss: 0.0060
Epoch 34/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1087 - loss: 0.0058 - val_RootMeanSquaredError: 0.1130 - val_loss: 0.0059
Epoch 35/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1094 - loss: 0.0058 - val_RootMeanSquaredError: 0.1124 - val_loss: 0.0058
Epoch 36/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1087 - loss: 0.0056 - val_RootMeanSquaredError: 0.1122 - val_loss: 0.0058
Epoch 37/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1053 - loss: 0.0054 - val_RootMeanSquaredError: 0.1118 - val_loss: 0.0058
Epoch 38/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1061 - loss: 0.0055 - val_RootMeanSquaredError: 0.1116 - val_loss: 0.0057
Epoch 39/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1082 - loss: 0.0056 - val_RootMeanSquaredError: 0.1113 - val_loss: 0.0057
Epoch 40/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - RootMeanSquaredError: 0.1074 - loss: 0.0056 - val_RootMeanSquaredError: 0.1111 - val_loss: 0.0057
Epoch 41/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1060 - loss: 0.0055 - val_RootMeanSquaredError: 0.1110 - val_loss: 0.0057
Epoch 42/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1042 - loss: 0.0053 - val_RootMeanSquaredError: 0.1107 - val_loss: 0.0056
Epoch 43/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 14ms/step - RootMeanSquaredError: 0.1092 - loss: 0.0057 - val_RootMeanSquaredError: 0.1106 - val_loss: 0.0056
Epoch 44/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1066 - loss: 0.0055 - val_RootMeanSquaredError: 0.1103 - val_loss: 0.0056
Epoch 45/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1039 - loss: 0.0054 - val_RootMeanSquaredError: 0.1103 - val_loss: 0.0056
Epoch 46/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.1053 - loss: 0.0055 - val_RootMeanSquaredError: 0.1100 - val_loss: 0.0056
Epoch 47/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1024 - loss: 0.0052 - val_RootMeanSquaredError: 0.1099 - val_loss: 0.0056
Epoch 48/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 14ms/step - RootMeanSquaredError: 0.1058 - loss: 0.0053 - val_RootMeanSquaredError: 0.1098 - val_loss: 0.0055
Epoch 49/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1073 - loss: 0.0054 - val_RootMeanSquaredError: 0.1097 - val_loss: 0.0055
Epoch 50/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1029 - loss: 0.0052 - val_RootMeanSquaredError: 0.1095 - val_loss: 0.0055
Epoch 51/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - RootMeanSquaredError: 0.1049 - loss: 0.0054 - val_RootMeanSquaredError: 0.1095 - val_loss: 0.0055
Epoch 52/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1071 - loss: 0.0055 - val_RootMeanSquaredError: 0.1095 - val_loss: 0.0055
Epoch 53/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1033 - loss: 0.0053 - val_RootMeanSquaredError: 0.1094 - val_loss: 0.0055
Epoch 54/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1046 - loss: 0.0054 - val_RootMeanSquaredError: 0.1092 - val_loss: 0.0055
Epoch 55/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1045 - loss: 0.0054 - val_RootMeanSquaredError: 0.1091 - val_loss: 0.0055
Epoch 56/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1022 - loss: 0.0051 - val_RootMeanSquaredError: 0.1091 - val_loss: 0.0055
Epoch 57/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - RootMeanSquaredError: 0.1025 - loss: 0.0050 - val_RootMeanSquaredError: 0.1090 - val_loss: 0.0054
Epoch 58/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - RootMeanSquaredError: 0.1022 - loss: 0.0052 - val_RootMeanSquaredError: 0.1094 - val_loss: 0.0055
Epoch 59/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1041 - loss: 0.0053 - val_RootMeanSquaredError: 0.1088 - val_loss: 0.0054
Epoch 60/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1024 - loss: 0.0051 - val_RootMeanSquaredError: 0.1089 - val_loss: 0.0054
Epoch 61/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1029 - loss: 0.0052 - val_RootMeanSquaredError: 0.1090 - val_loss: 0.0054
Epoch 62/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1027 - loss: 0.0052 - val_RootMeanSquaredError: 0.1087 - val_loss: 0.0054
Epoch 63/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1031 - loss: 0.0052 - val_RootMeanSquaredError: 0.1085 - val_loss: 0.0054
Epoch 64/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1029 - loss: 0.0052 - val_RootMeanSquaredError: 0.1087 - val_loss: 0.0054
Epoch 65/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1058 - loss: 0.0053 - val_RootMeanSquaredError: 0.1085 - val_loss: 0.0054
Epoch 66/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1016 - loss: 0.0051 - val_RootMeanSquaredError: 0.1089 - val_loss: 0.0054
Epoch 67/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1014 - loss: 0.0049 - val_RootMeanSquaredError: 0.1083 - val_loss: 0.0054
Epoch 68/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1017 - loss: 0.0051 - val_RootMeanSquaredError: 0.1082 - val_loss: 0.0054
Epoch 69/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1004 - loss: 0.0050 - val_RootMeanSquaredError: 0.1088 - val_loss: 0.0054
Epoch 70/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1038 - loss: 0.0051 - val_RootMeanSquaredError: 0.1081 - val_loss: 0.0053
Epoch 71/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1023 - loss: 0.0051 - val_RootMeanSquaredError: 0.1089 - val_loss: 0.0054
Epoch 72/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.1018 - loss: 0.0051 - val_RootMeanSquaredError: 0.1081 - val_loss: 0.0053
Epoch 73/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1023 - loss: 0.0052 - val_RootMeanSquaredError: 0.1083 - val_loss: 0.0054
Epoch 74/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1084 - val_loss: 0.0054
Epoch 75/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.1014 - loss: 0.0051 - val_RootMeanSquaredError: 0.1080 - val_loss: 0.0053
Epoch 76/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.1008 - loss: 0.0050 - val_RootMeanSquaredError: 0.1081 - val_loss: 0.0053
Epoch 77/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1043 - loss: 0.0052 - val_RootMeanSquaredError: 0.1078 - val_loss: 0.0053
Epoch 78/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0989 - loss: 0.0049 - val_RootMeanSquaredError: 0.1079 - val_loss: 0.0053
Epoch 79/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1040 - loss: 0.0051 - val_RootMeanSquaredError: 0.1080 - val_loss: 0.0053
Epoch 80/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1030 - loss: 0.0051 - val_RootMeanSquaredError: 0.1077 - val_loss: 0.0053
Epoch 81/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1077 - val_loss: 0.0053
Epoch 82/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1013 - loss: 0.0051 - val_RootMeanSquaredError: 0.1078 - val_loss: 0.0053
Epoch 83/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0997 - loss: 0.0049 - val_RootMeanSquaredError: 0.1076 - val_loss: 0.0053
Epoch 84/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1016 - loss: 0.0051 - val_RootMeanSquaredError: 0.1076 - val_loss: 0.0053
Epoch 85/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1008 - loss: 0.0050 - val_RootMeanSquaredError: 0.1076 - val_loss: 0.0053
Epoch 86/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1020 - loss: 0.0050 - val_RootMeanSquaredError: 0.1075 - val_loss: 0.0053
Epoch 87/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - RootMeanSquaredError: 0.0989 - loss: 0.0049 - val_RootMeanSquaredError: 0.1080 - val_loss: 0.0053
Epoch 88/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1002 - loss: 0.0049 - val_RootMeanSquaredError: 0.1075 - val_loss: 0.0053
Epoch 89/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - RootMeanSquaredError: 0.1001 - loss: 0.0049 - val_RootMeanSquaredError: 0.1075 - val_loss: 0.0053
Epoch 90/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1075 - val_loss: 0.0053
Epoch 91/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1036 - loss: 0.0050 - val_RootMeanSquaredError: 0.1074 - val_loss: 0.0053
Epoch 92/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1027 - loss: 0.0051 - val_RootMeanSquaredError: 0.1074 - val_loss: 0.0053
Epoch 93/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1076 - val_loss: 0.0053
Epoch 94/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1073 - val_loss: 0.0053
Epoch 95/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1023 - loss: 0.0050 - val_RootMeanSquaredError: 0.1074 - val_loss: 0.0053
Epoch 96/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1032 - loss: 0.0051 - val_RootMeanSquaredError: 0.1074 - val_loss: 0.0053
Epoch 97/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1010 - loss: 0.0050 - val_RootMeanSquaredError: 0.1075 - val_loss: 0.0053
Epoch 98/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1008 - loss: 0.0050 - val_RootMeanSquaredError: 0.1077 - val_loss: 0.0053
Epoch 99/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 13ms/step - RootMeanSquaredError: 0.1011 - loss: 0.0051 - val_RootMeanSquaredError: 0.1073 - val_loss: 0.0053
Epoch 100/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.0987 - loss: 0.0049 - val_RootMeanSquaredError: 0.1073 - val_loss: 0.0053
Epoch 101/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.0992 - loss: 0.0049 - val_RootMeanSquaredError: 0.1072 - val_loss: 0.0052
Epoch 102/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - RootMeanSquaredError: 0.0985 - loss: 0.0048 - val_RootMeanSquaredError: 0.1087 - val_loss: 0.0054
Epoch 103/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1013 - loss: 0.0051 - val_RootMeanSquaredError: 0.1074 - val_loss: 0.0053
Epoch 104/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - RootMeanSquaredError: 0.1019 - loss: 0.0051 - val_RootMeanSquaredError: 0.1083 - val_loss: 0.0054
Epoch 105/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1034 - loss: 0.0050 - val_RootMeanSquaredError: 0.1077 - val_loss: 0.0053
Epoch 106/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1044 - loss: 0.0052 - val_RootMeanSquaredError: 0.1072 - val_loss: 0.0052
Epoch 107/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1017 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 108/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1001 - loss: 0.0049 - val_RootMeanSquaredError: 0.1073 - val_loss: 0.0053
Epoch 109/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1072 - val_loss: 0.0052
Epoch 110/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1003 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 111/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 112/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1002 - loss: 0.0050 - val_RootMeanSquaredError: 0.1070 - val_loss: 0.0052
Epoch 113/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1029 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 114/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1016 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 115/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1027 - loss: 0.0051 - val_RootMeanSquaredError: 0.1075 - val_loss: 0.0053
Epoch 116/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 117/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1003 - loss: 0.0050 - val_RootMeanSquaredError: 0.1070 - val_loss: 0.0052
Epoch 118/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.0997 - loss: 0.0049 - val_RootMeanSquaredError: 0.1073 - val_loss: 0.0053
Epoch 119/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1002 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 120/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 121/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1004 - loss: 0.0050 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 122/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.0992 - loss: 0.0048 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 123/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.0994 - loss: 0.0049 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 124/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1041 - loss: 0.0051 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 125/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.0973 - loss: 0.0047 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 126/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1019 - loss: 0.0050 - val_RootMeanSquaredError: 0.1074 - val_loss: 0.0053
Epoch 127/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - RootMeanSquaredError: 0.1019 - loss: 0.0052 - val_RootMeanSquaredError: 0.1070 - val_loss: 0.0052
Epoch 128/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1011 - loss: 0.0050 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 129/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1033 - loss: 0.0050 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 130/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 19ms/step - RootMeanSquaredError: 0.1001 - loss: 0.0049 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 131/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - RootMeanSquaredError: 0.0992 - loss: 0.0048 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 132/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.1017 - loss: 0.0050 - val_RootMeanSquaredError: 0.1070 - val_loss: 0.0052
Epoch 133/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.1024 - loss: 0.0051 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 134/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 19ms/step - RootMeanSquaredError: 0.1003 - loss: 0.0049 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 135/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1006 - loss: 0.0050 - val_RootMeanSquaredError: 0.1079 - val_loss: 0.0053
Epoch 136/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1010 - loss: 0.0050 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 137/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0990 - loss: 0.0049 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 138/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.1019 - loss: 0.0050 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 139/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1034 - loss: 0.0050 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 140/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0989 - loss: 0.0049 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 141/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 142/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.1009 - loss: 0.0050 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 143/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0980 - loss: 0.0048 - val_RootMeanSquaredError: 0.1070 - val_loss: 0.0052
Epoch 144/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0995 - loss: 0.0049 - val_RootMeanSquaredError: 0.1069 - val_loss: 0.0052
Epoch 145/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0998 - loss: 0.0050 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 146/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0993 - loss: 0.0049 - val_RootMeanSquaredError: 0.1073 - val_loss: 0.0053
Epoch 147/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.0984 - loss: 0.0048 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 148/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0994 - loss: 0.0049 - val_RootMeanSquaredError: 0.1078 - val_loss: 0.0053
Epoch 149/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0997 - loss: 0.0049 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 150/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1009 - loss: 0.0050 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 151/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0970 - loss: 0.0047 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 152/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0991 - loss: 0.0049 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 153/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0988 - loss: 0.0048 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 154/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0991 - loss: 0.0048 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 155/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.0998 - loss: 0.0049 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 156/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1023 - loss: 0.0051 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 157/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step - RootMeanSquaredError: 0.0995 - loss: 0.0048 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 158/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 159/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.0989 - loss: 0.0048 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 160/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.0982 - loss: 0.0048 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 161/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - RootMeanSquaredError: 0.0995 - loss: 0.0049 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 162/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 19ms/step - RootMeanSquaredError: 0.1011 - loss: 0.0051 - val_RootMeanSquaredError: 0.1070 - val_loss: 0.0052
Epoch 163/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 164/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1011 - loss: 0.0050 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 165/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0982 - loss: 0.0048 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 166/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0984 - loss: 0.0048 - val_RootMeanSquaredError: 0.1071 - val_loss: 0.0052
Epoch 167/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0993 - loss: 0.0049 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 168/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0991 - loss: 0.0049 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 169/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1017 - loss: 0.0051 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 170/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0995 - loss: 0.0049 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 171/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1015 - loss: 0.0051 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 172/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0998 - loss: 0.0049 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 173/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0990 - loss: 0.0048 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 174/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1010 - loss: 0.0050 - val_RootMeanSquaredError: 0.1068 - val_loss: 0.0052
Epoch 175/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1001 - loss: 0.0050 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 176/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.0980 - loss: 0.0047 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 177/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - RootMeanSquaredError: 0.0989 - loss: 0.0049 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0052
Epoch 178/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0050 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 179/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.1010 - loss: 0.0049 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0052
Epoch 180/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0049 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 181/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0990 - loss: 0.0048 - val_RootMeanSquaredError: 0.1072 - val_loss: 0.0052
Epoch 182/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1007 - loss: 0.0050 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 183/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.0995 - loss: 0.0048 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 184/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 19ms/step - RootMeanSquaredError: 0.0992 - loss: 0.0049 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 185/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - RootMeanSquaredError: 0.0988 - loss: 0.0049 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0052
Epoch 186/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - RootMeanSquaredError: 0.1004 - loss: 0.0049 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0052
Epoch 187/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - RootMeanSquaredError: 0.0977 - loss: 0.0048 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 188/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 18ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0049 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0052
Epoch 189/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0979 - loss: 0.0047 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 190/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0999 - loss: 0.0048 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0052
Epoch 191/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.1005 - loss: 0.0049 - val_RootMeanSquaredError: 0.1066 - val_loss: 0.0052
Epoch 192/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0993 - loss: 0.0049 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 193/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0991 - loss: 0.0049 - val_RootMeanSquaredError: 0.1065 - val_loss: 0.0052
Epoch 194/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - RootMeanSquaredError: 0.0983 - loss: 0.0048 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0051
Epoch 195/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0987 - loss: 0.0048 - val_RootMeanSquaredError: 0.1063 - val_loss: 0.0051
Epoch 196/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - RootMeanSquaredError: 0.0987 - loss: 0.0048 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0051
Epoch 197/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - RootMeanSquaredError: 0.0995 - loss: 0.0049 - val_RootMeanSquaredError: 0.1063 - val_loss: 0.0051
Epoch 198/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.1002 - loss: 0.0049 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0051
Epoch 199/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - RootMeanSquaredError: 0.0968 - loss: 0.0047 - val_RootMeanSquaredError: 0.1067 - val_loss: 0.0052
Epoch 200/200
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - RootMeanSquaredError: 0.0981 - loss: 0.0048 - val_RootMeanSquaredError: 0.1064 - val_loss: 0.0051





<keras.src.callbacks.history.History at 0x7d861f1f72b0>

plt.plot(model.history.history['val_RootMeanSquaredError'][10:], label='Validation RMSE')
plt.plot(model.history.history['RootMeanSquaredError'][10:], label = 'Learning RMSE')

plt.legend()
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.title('Learning Curve for NN model 3')

plt.show()

png

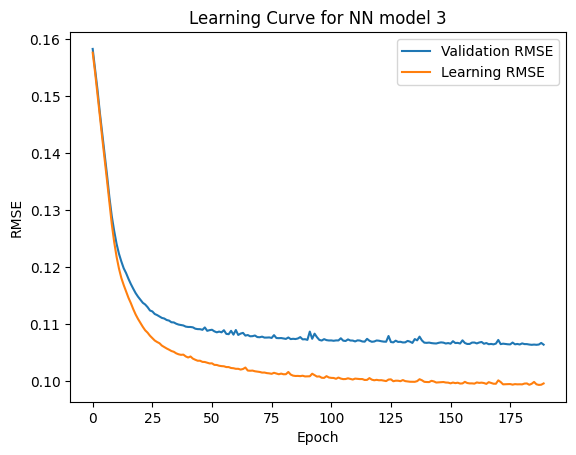
Comparison of predicted vs observed events for storm AL152023

test_data_scaled = model_scaled[model_scaled.id == "AL152023"]
test_data = df_NN_3[df_NN_3.id == "AL152023"]

model_pred = []

for idx in range(len(test_data_scaled) - window_size):
    window = test_data_scaled.iloc[idx : idx + window_size + 1, :][::-1]
    for offset in range(1, window_size + 1):
        shifted = window.shift(-offset)
        for col in window_cols:
            window[f"{col}-{offset}"] = shifted[col]
    window.drop(columns=window_cols+["id","time"],inplace=True)
    model_pred.append(model.predict(window.iloc[[0]].values.reshape((1,1,16))))
model_pred = np.array(model_pred).squeeze()

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 173ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step

unscaled_lat = model_pred[:,0]*col_maxs["lat_0"] + col_mins["lat_0"]
unscaled_lon = model_pred[:,1]*col_maxs["lon_0"] + col_mins["lon_0"]

model_len = model_pred.shape[0]
plt.figure()
plt.plot(test_data.time.values,test_data_scaled.lat_0.values, label="Observed scaled Latitude")
plt.scatter(test_data.time.values[-model_len:], model_pred[:,0], marker="x", color="r", label="Model data scaled Latitude")
plt.title("Model vs Observed Scaled Latitude for Storm AL202023")
plt.ylabel
plt.legend()

<matplotlib.legend.Legend at 0x7d861eff3a00>

png

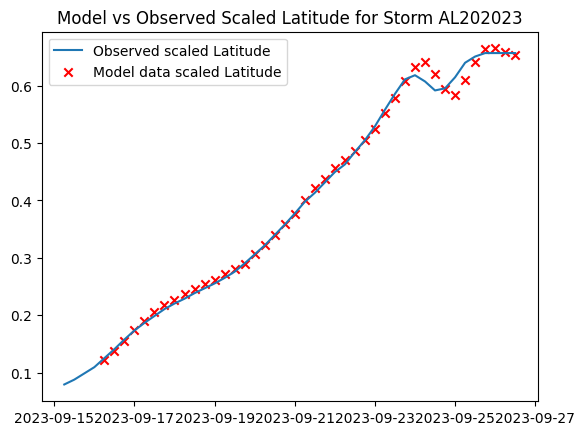
plt.figure()
plt.plot(test_data.time.values,test_data_scaled.lon_0.values, label="Observed scaled Longitude")
plt.scatter(test_data.time.values[-model_len:], model_pred[:,1], marker="x", color="r", label="Model data scaled Longitude")
plt.title("Model vs Observed Scaled Longitude for Storm AL202023")
plt.ylabel
plt.legend()

<matplotlib.legend.Legend at 0x7d861670ae60>

png

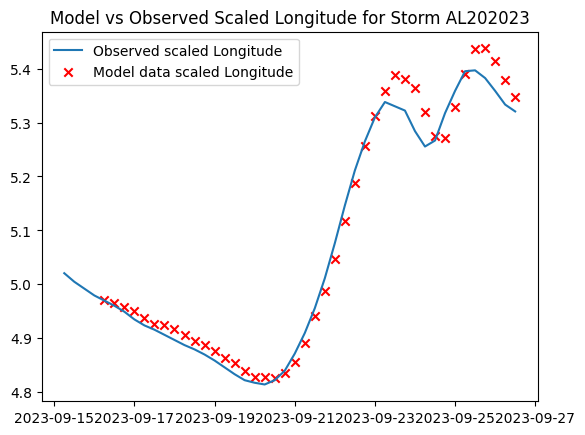
fig = plt.figure(figsize=(10, 8))
ax = plt.axes(projection=ccrs.PlateCarree())
ax.coastlines()
storm=df_NN_3.loc[df_NN_3.id=="AL152023"]
plt.plot(storm.lon_0,storm.lat_0, label="Observed AL152023 Hurricane Track")
plt.plot(unscaled_lon, unscaled_lat, label="Modeled AL152023 Hurricane Track")
plt.legend()

<matplotlib.legend.Legend at 0x7d86164356c0>

png

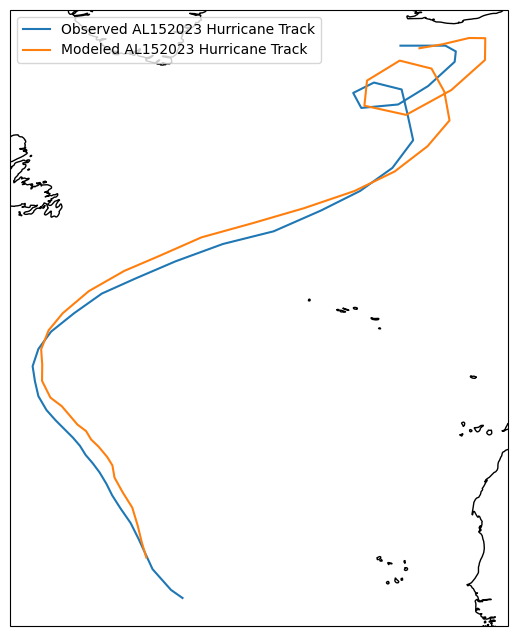
Model Building - Regression

cols = {'X0':'time',
        'X1':'hour',
        'X2':'identifier',
        'X3':'status_of_system',
        'X6':'maximum_sustained_wind',
        'X7':'minimum_pressure',
        'X8':'34kt_max_ext_ne_quad',
        'X9':'34kt_max_ext_se_quad',
        'X10':'34kt_max_ext_sw_quad',
        'X11':'34kt_max_ext_nw_quad',
        'X12':'50kt_max_ext_ne_quad',
        'X13':'50kt_max_ext_se_quad',
        'X14':'50kt_max_ext_sw_quad',
        'X15':'50kt_max_ext_nw_quad',
        'X16':'64kt_max_ext_ne_quad',
        'X17':'64kt_max_ext_se_quad',
        'X18':'64kt_max_ext_sw_quad',
        'X19':'64kt_max_ext_nw_quad',
        'X20':'rad_of_max_wind'}

df_RR = df.rename(columns=cols)

df_RR.columns

Index(['id', 'name', 'time', 'hour', 'identifier', 'status_of_system',
       'latitude', 'longitude', 'maximum_sustained_wind', 'minimum_pressure',
       '34kt_max_ext_ne_quad', '34kt_max_ext_se_quad', '34kt_max_ext_sw_quad',
       '34kt_max_ext_nw_quad', '50kt_max_ext_ne_quad', '50kt_max_ext_se_quad',
       '50kt_max_ext_sw_quad', '50kt_max_ext_nw_quad', '64kt_max_ext_ne_quad',
       '64kt_max_ext_se_quad', '64kt_max_ext_sw_quad', '64kt_max_ext_nw_quad',
       'rad_of_max_wind', 'year', 'month', 'day'],
      dtype='object')

# Features to drop

feature_to_drop = ['id', 'name', 'time', 'hour', 'identifier']
df_RR.drop(feature_to_drop, axis=1, inplace=True)

ohe = OneHotEncoder()
feature_to_encode = ['status_of_system']

df_tmp = df_RR[feature_to_encode]
data = ohe.fit_transform(df_tmp)

df_tmp = pd.DataFrame(data.toarray(), columns=ohe.get_feature_names_out(), dtype=int)
df_RR.drop(feature_to_encode, axis=1, inplace=True)
df_RR = pd.concat([df_RR, df_tmp], axis=1)

# process features by normalization

mms = MinMaxScaler()
feature_to_scale = ['latitude', 'longitude', 'maximum_sustained_wind', 'minimum_pressure',
                    '34kt_max_ext_ne_quad', '34kt_max_ext_se_quad', '34kt_max_ext_sw_quad', '34kt_max_ext_nw_quad',
                    '50kt_max_ext_ne_quad', '50kt_max_ext_se_quad', '50kt_max_ext_sw_quad', '50kt_max_ext_nw_quad',
                    '64kt_max_ext_ne_quad', '64kt_max_ext_se_quad', '64kt_max_ext_sw_quad', '64kt_max_ext_nw_quad',
                    'rad_of_max_wind']

for _ in feature_to_scale:
  df_RR[[_]] = mms.fit_transform(df_RR[[_]])

df_RR.head()
latitude longitude maximum_sustained_wind minimum_pressure 34kt_max_ext_ne_quad 34kt_max_ext_se_quad 34kt_max_ext_sw_quad 34kt_max_ext_nw_quad 50kt_max_ext_ne_quad 50kt_max_ext_se_quad ... day status_of_system_DB status_of_system_EX status_of_system_HU status_of_system_LO status_of_system_SD status_of_system_SS status_of_system_TD status_of_system_TS status_of_system_WV
0 0.276316 0.625623 0.67803 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 25 0 0 1 0 0 0 0 0 0
1 0.276316 0.624199 0.67803 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 25 0 0 1 0 0 0 0 0 0
2 0.276316 0.622776 0.67803 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 25 0 0 1 0 0 0 0 0 0
3 0.277632 0.621590 0.67803 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 25 0 0 1 0 0 0 0 0 0
4 0.278947 0.620878 0.67803 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 25 0 0 1 0 0 0 0 0 0

5 rows × 29 columns

X = df_RR.iloc[:, 2:]
y = df_RR.iloc[:, :2].astype('float')

X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=1234)
y_train_lat = y_train.iloc[:, 0]
y_train_lon = y_train.iloc[:, 1]
y_test_lat = y_test.iloc[:, 0]
y_test_lon = y_test.iloc[:, 1]

X_train.shape, X_test.shape, y_train_lat.shape, y_test_lat.shape, y_train_lon.shape, y_test_lon.shape

((38324, 27), (16425, 27), (38324,), (16425,), (38324,), (16425,))

from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn import svm
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, r2_score

# Linear Regression

lr_lat = LinearRegression()
lr_lat.fit(X_train, y_train_lat)
y_pred_lat = lr_lat.predict(X_test)

lr_lon = LinearRegression()
lr_lon.fit(X_train, y_train_lon)
y_pred_lon = lr_lon.predict(X_test)

print("- Latitude by Linear Regression")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

print("- Longitude by Linear Regression")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Linear Regression
RMSE = 0.10633753591978912
R^2 = 0.38983133767971667
- Longitude by Linear Regression
RMSE = 0.045391889122120097
R^2 = 0.1301975162235809

# SGD

sgd_lat = SGDRegressor(max_iter=1000, tol=1e-3)
sgd_lat.fit(X_train, y_train_lat)
y_pred_lat = sgd_lat.predict(X_test)

print("- Latitude by SGD")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

sgd_lon = SGDRegressor(max_iter=1000, tol=1e-3)
sgd_lon.fit(X_train, y_train_lon)
y_pred_lon = sgd_lon.predict(X_test)

print("- Longitude by SGD")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")


- Latitude by SGD
RMSE = 81375967824712.55
R^2 = -3.5732964463883664e+29
- Longitude by SGD
RMSE = 662448442565931.4
R^2 = -1.852542990308599e+32

# Decision Tree

dt_lat = DecisionTreeRegressor()
dt_lat.fit(X_train, y_train_lat)
y_pred_lat = dt_lat.predict(X_test)

print("- Latitude by Decision Tree")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

dt_lon = DecisionTreeRegressor()
dt_lon.fit(X_train, y_train_lon)
y_pred_lon = dt_lon.predict(X_test)

print("- Longitude by Decision Tree")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Decision Tree
RMSE = 0.07253254851742584
R^2 = 0.7161149068403039
- Longitude by Decision Tree
RMSE = 0.029939092226239073
R^2 = 0.6216084891916902

# Random Forest

rf_lat = RandomForestRegressor(random_state=1)
rf_lat.fit(X_train, y_train_lat)
y_pred_lat = rf_lat.predict(X_test)

print("- Latitude by Random Forest")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

rf_lon = RandomForestRegressor(random_state=1)
rf_lon.fit(X_train, y_train_lon)
y_pred_lon = rf_lon.predict(X_test)

print("- Longitude by Random Forest")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Random Forest
RMSE = 0.05636705229006893
R^2 = 0.828553998070632
- Longitude by Random Forest
RMSE = 0.022274719203831703
R^2 = 0.7905460262061337

# Gradient Boosting

gb_lat = GradientBoostingRegressor(random_state=1)
gb_lat.fit(X_train, y_train_lat)
y_pred_lat = gb_lat.predict(X_test)

print("- Latitude by Gradient Boosting")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

gb_lon = GradientBoostingRegressor(random_state=1)
gb_lon.fit(X_train, y_train_lon)
y_pred_lon = gb_lon.predict(X_test)

print("- Longitude by Gradient Boosting")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Gradient Boosting
RMSE = 0.1002774188971752
R^2 = 0.45739597923972075
- Longitude by Gradient Boosting
RMSE = 0.042253619963897406
R^2 = 0.24631135545457417

# SVM

svm_lat = svm.SVR()
svm_lat.fit(X_train, y_train_lat)
y_pred_lat = svm_lat.predict(X_test)

print("- Latitude by SVM")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

svm_lon = svm.SVR()
svm_lon.fit(X_train, y_train_lon)
y_pred_lon = svm_lon.predict(X_test)

print("- Longitude by SVM")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by SVM
RMSE = 0.1361498621777826
R^2 = -0.000255909803139831
- Longitude by SVM
RMSE = 0.052696516052692335
R^2 = -0.17227076728839075

Reduced Feature Dimension

from sklearn.decomposition import PCA

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X)
X_reduced = pd.DataFrame(data=X_reduced, index=X.index)

print("Dimension before PCA:", X.shape)
print("Dimension after PCA:", X_reduced.shape)

X_reduced.head()

Dimension before PCA: (54749, 27)
Dimension after PCA: (54749, 1)
0
0 105.281105
1 105.281105
2 105.281105
3 105.281105
4 105.281105 
# linear regression

lr_lat = LinearRegression()
lr_lat.fit(X_train, y_train_lat)
y_pred_lat = lr_lat.predict(X_test)

print("- Latitude by Linear Regression")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

lr_lon = LinearRegression()
lr_lon.fit(X_train, y_train_lon)
y_pred_lon = lr_lon.predict(X_test)

print("- Longitude by Linear Regression")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Linear Regression
RMSE = 0.10633753591978912
R^2 = 0.38983133767971667
- Longitude by Linear Regression
RMSE = 0.045391889122120097
R^2 = 0.1301975162235809

# SGD

sgd_lat = SGDRegressor(max_iter=1000, tol=1e-3)
sgd_lat.fit(X_train, y_train_lat)
y_pred_lat = sgd_lat.predict(X_test)

print("- Latitude by SGD")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

sgd_lon = SGDRegressor(max_iter=1000, tol=1e-3)
sgd_lon.fit(X_train, y_train_lon)
y_pred_lon = sgd_lon.predict(X_test)

print("- Longitude by SGD")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by SGD
RMSE = 244756496080594.0
R^2 = -3.232549384051073e+30
- Longitude by SGD
RMSE = 220223810656020.84
R^2 = -2.0473527430006712e+31

# Decision Tree

dt_lat = DecisionTreeRegressor()
dt_lat.fit(X_train, y_train_lat)
y_pred_lat = dt_lat.predict(X_test)

print("- Latitude by Decision Tree")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

dt_lon = DecisionTreeRegressor()
dt_lon.fit(X_train, y_train_lon)
y_pred_lon = dt_lon.predict(X_test)

print("- Longitude by Decision Tree")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Decision Tree
RMSE = 0.07224777360437251
R^2 = 0.7183396914952187
- Longitude by Decision Tree
RMSE = 0.029824056699133135
R^2 = 0.6245107042257154

# Random Forest

rf_lat = RandomForestRegressor(random_state=1)
rf_lat.fit(X_train, y_train_lat)
y_pred_lat = rf_lat.predict(X_test)

print("- Latitude by Random Forest")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

rf_lon = RandomForestRegressor(random_state=1)
rf_lon.fit(X_train, y_train_lon)
y_pred_lon = rf_lon.predict(X_test)

print("- Longitude by Random Forest")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Random Forest
RMSE = 0.05636705229006893
R^2 = 0.828553998070632
- Longitude by Random Forest
RMSE = 0.022274719203831703
R^2 = 0.7905460262061337

# Gradient Boosting

gb_lat = GradientBoostingRegressor(random_state=1)
gb_lat.fit(X_train, y_train_lat)
y_pred_lat = gb_lat.predict(X_test)

print("- Latitude by Gradient Boosting")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

gb_lon = GradientBoostingRegressor(random_state=1)
gb_lon.fit(X_train, y_train_lon)
y_pred_lon = gb_lon.predict(X_test)

print("- Longitude by Gradient Boosting")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by Gradient Boosting
RMSE = 0.1002774188971752
R^2 = 0.45739597923972075
- Longitude by Gradient Boosting
RMSE = 0.042253619963897406
R^2 = 0.24631135545457417

# SVM

svm_lat = svm.SVR()
svm_lat.fit(X_train, y_train_lat)
y_pred_lat = svm_lat.predict(X_test)

print("- Latitude by SVM")
print(f"RMSE = {pow(mean_squared_error(y_test_lat, y_pred_lat), 0.5)}")
print(f"R^2 = {r2_score(y_test_lat, y_pred_lat)}")

svm_lon = svm.SVR()
svm_lon.fit(X_train, y_train_lon)
y_pred_lon = svm_lon.predict(X_test)

print("- Longitude by SVM")
print(f"RMSE = {pow(mean_squared_error(y_test_lon, y_pred_lon), 0.5)}")
print(f"R^2 = {r2_score(y_test_lon, y_pred_lon)}")

- Latitude by SVM
RMSE = 0.1361498621777826
R^2 = -0.000255909803139831
- Longitude by SVM
RMSE = 0.052696516052692335
R^2 = -0.17227076728839075